题目内容
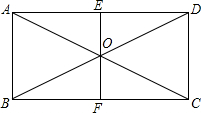 如图,点O为矩形ABCD对角线的交点,过点O作EF⊥BC于点F,若AB=2cm,BC=4cm,求四边形AECF的面积.
如图,点O为矩形ABCD对角线的交点,过点O作EF⊥BC于点F,若AB=2cm,BC=4cm,求四边形AECF的面积.考点:矩形的性质
专题:
分析:如图,连接AF、EC.由矩形的性质得到点E、F分别是AD、BC的中点,则由直角三角形的面积公式进行解答即可.
解答: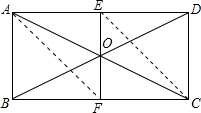 解:如图,连接AF、EC.
解:如图,连接AF、EC.
∵四边形ABCD是矩形,且点O为矩形ABCD对角线的交点,
∴AD∥BC,AB⊥BC,DC⊥BC,点O是AC或BD的中点,
又∵过点O作EF⊥BC于点F,
∴EF∥AB∥CD,
∴点E、F分别是AD、BC的中点,
∴AE=CF,
∴四边形AECF是平行四边形,
又∵AB=2cm,BC=4cm,
∴S四边形AECF=AE•EF=
BC•AB=
×4×2=4(cm2)
即四边形AECF的面积是4cm2.
 解:如图,连接AF、EC.
解:如图,连接AF、EC.∵四边形ABCD是矩形,且点O为矩形ABCD对角线的交点,
∴AD∥BC,AB⊥BC,DC⊥BC,点O是AC或BD的中点,
又∵过点O作EF⊥BC于点F,
∴EF∥AB∥CD,
∴点E、F分别是AD、BC的中点,
∴AE=CF,
∴四边形AECF是平行四边形,
又∵AB=2cm,BC=4cm,
∴S四边形AECF=AE•EF=
| 1 |
| 2 |
| 1 |
| 2 |
即四边形AECF的面积是4cm2.
点评:本题主要考查了矩形的性质,主要分两步进行,先证明四边形AECF是平行四边形,然后利用矩形的性质求得相关线段的长度并代入平行四边形的面积公式进行解答即可.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
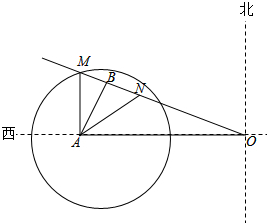 如图,学校A位于工地O的正西方向240米,拖拉机从O出发,沿大路以5米每秒的速度沿北偏西60°方向行使,拖拉机的噪声影响半径为130米,那么大路上行驶的拖拉机的噪声会影响学校吗?如果有影响会有多长时间?
如图,学校A位于工地O的正西方向240米,拖拉机从O出发,沿大路以5米每秒的速度沿北偏西60°方向行使,拖拉机的噪声影响半径为130米,那么大路上行驶的拖拉机的噪声会影响学校吗?如果有影响会有多长时间?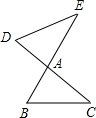 如图,线段BE、CD相交于点A,连接DE、BC,请添加一个条件,使△ADE与△ABC相似,且点B的对应点为点D,这个条件可以是
如图,线段BE、CD相交于点A,连接DE、BC,请添加一个条件,使△ADE与△ABC相似,且点B的对应点为点D,这个条件可以是 如图,在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE,求证:AE=BE+GE.
如图,在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE,求证:AE=BE+GE.