题目内容
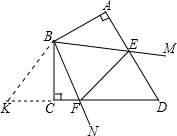 已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,将∠MBN绕点B旋转.当∠MBN旋转到如图的位置,此时∠MBN的两边分别交AD、DC于E、F,且AE≠CF.延长DC至点K,使CK=AE,连接BK.求证:
(1)△ABE≌△CBK;
(2)∠KBC+∠CBF=60°;
(3)CF+AE=EF.
考点:旋转的性质,全等三角形的判定与性质
专题:
分析:(1)根据已知条件可以利用SAS证明△ABE≌△CBK;
(2)由(1)可得∠KBF=∠EBF=60°,即∠KBC+∠CBF=60°;
(3)再证明△EBF≌△KBF,即可得EF=CK+CF,可证AE+CF=EF.
(2)由(1)可得∠KBF=∠EBF=60°,即∠KBC+∠CBF=60°;
(3)再证明△EBF≌△KBF,即可得EF=CK+CF,可证AE+CF=EF.
解答:证明:(1)在△ABE和△CBK中,
,
∴△ABE≌△CBK(SAS).
(2)∵△ABE≌△CBK,
∴BE=BK,∠ABE=∠KBC,
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,
即∠KBE=120°,
∵∠EBF=60°,
∴∠KBF=∠EBF=60°.
∴∠KBC+∠CBF=60°;
(3)在△EBF和△KBF中,
,
∴△EBF≌△KBF(SAS).
∴EF=KF.
∴EF=CK+CF.
∴AE+CF=EF.
|
∴△ABE≌△CBK(SAS).
(2)∵△ABE≌△CBK,
∴BE=BK,∠ABE=∠KBC,
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,
即∠KBE=120°,
∵∠EBF=60°,
∴∠KBF=∠EBF=60°.
∴∠KBC+∠CBF=60°;
(3)在△EBF和△KBF中,
|
∴△EBF≌△KBF(SAS).
∴EF=KF.
∴EF=CK+CF.
∴AE+CF=EF.
点评:本题主要考查了旋转的性质以及全等三角形的判定方法,常用的方法有SSS,SAS,AAS等,这些方法要求学生能够掌握并灵活运用.

练习册系列答案
相关题目
用同一种正多边形地砖不能镶嵌成平整的地面的是( )
| A、正三角形地砖 |
| B、正方形地砖 |
| C、正五边形地砖 |
| D、正六边形地砖 |
将下列各组数据作为三角形的边长,能够组成直角三角形的是( )
| A、4,5,6 | ||
| B、1.5,2,2.5 | ||
| C、2,3,4 | ||
D、1,
|
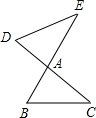 如图,线段BE、CD相交于点A,连接DE、BC,请添加一个条件,使△ADE与△ABC相似,且点B的对应点为点D,这个条件可以是
如图,线段BE、CD相交于点A,连接DE、BC,请添加一个条件,使△ADE与△ABC相似,且点B的对应点为点D,这个条件可以是
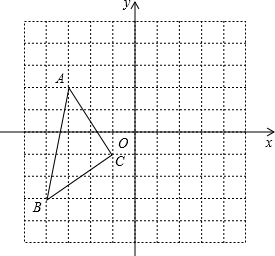 (1)如图,写出点A,B,C的坐标A
(1)如图,写出点A,B,C的坐标A 如图,点E是?ABCD中的边BC上的一点,AE交BD于点F,BE=3,BC=4,S△FBE=18,求?ABCD的面积.
如图,点E是?ABCD中的边BC上的一点,AE交BD于点F,BE=3,BC=4,S△FBE=18,求?ABCD的面积.