题目内容
2．设-$\sqrt{2}$对应数轴上点A，$\sqrt{3}$对应数轴上点B，那么A、B两点间的距离是$\sqrt{3}$+$\sqrt{2}$．分析 结合数轴根据数轴上两点间的距离公式即可解答．
解答 解：∵-$\sqrt{2}$对应数轴上点A，$\sqrt{3}$对应数轴上点B，
∴A，B两点间的距离是AB=$\sqrt{3}$+$\sqrt{2}$．
故答案为：$\sqrt{3}$+$\sqrt{2}$．
点评 此题主要考查了实数与数轴之间的对应关系，解答此题的关键是能够熟练计算数轴上两点间的距离．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
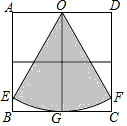如图，四个小正方形的边长都是1，若以O为圆心，OG为半径作弧分别交AB、DC于点E、F，则图中阴影部分的面积为$\frac{2π}{3}$．
17．下列函数中，不是二次函数的是（ ）
| A． | y=1-$\sqrt{2}$x2 | B． | y=2（x-1）2+4 | C． | y=$\frac{1}{2}$（x-1）（x+4） | D． | y=（x-2）2-x2 |
如图，△ABC是等腰三角形，AD是底边BC上的高，若AB=5cm，BD=4cm，则△ABC的周长是18cm．