题目内容
10.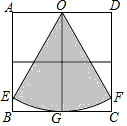 如图,四个小正方形的边长都是1,若以O为圆心,OG为半径作弧分别交AB、DC于点E、F,则图中阴影部分的面积为$\frac{2π}{3}$.
如图,四个小正方形的边长都是1,若以O为圆心,OG为半径作弧分别交AB、DC于点E、F,则图中阴影部分的面积为$\frac{2π}{3}$.
分析 先根据OD=$\frac{1}{2}$OF得出∠DOF=60°,同理可得出∠AOE=60°,进而得出∠EOF的度数,根据扇形的面积公式即可得出结论.
解答 解:∵OD=1,OF=OG=2,
∴cos∠DOF=$\frac{OD}{OF}$=$\frac{1}{2}$,
∴∠DOF=60°.
同理,∠AOE=60°,
∴∠EOF=180°-60°-60°=60°,
∴图中阴影部分的面积=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
19.⊙O中,M为$\widehat{AB}$的中点,则下列结论正确的是( )
| A. | ∠AOB>2∠AOM | B. | ∠AOB=2∠AOM | ||
| C. | ∠AOB<2∠AOM | D. | ∠AOB与2∠AOM的大小不能确定 |
1.方程组$\left\{\begin{array}{l}{4x+3y=1}\\{kx+(k-1)y-3=0}\end{array}\right.$的解x和y的值相等,则k的值等于( )
| A. | 4 | B. | 10 | C. | 11 | D. | 12 |
5.一个三位数,a表百位数,b表示十位数,c表示个位数,那么这个三位数可表示为( )
| A. | a+b+c | B. | abc | C. | 10abc | D. | 100a+10b+c |