题目内容
15.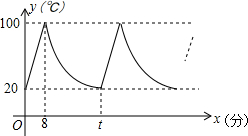 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?
分析 (1)利用待定系数法代入函数解析式求出即可;
(2)首先求出反比例函数解析式进而得出t的值;
(3)利用已知由x=5代入求出饮水机内的温度即可.
解答 解:(1)当0≤x≤8时,设水温y(℃)与开机时间x(分)的函数关系为:y=kx+b,
依据题意,得$\left\{\begin{array}{l}{b=20}\\{8k+b=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=10}\\{b=20}\end{array}\right.$,
故此函数解析式为:y=10x+20;
(2)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为:y=$\frac{m}{x}$,
依据题意,得:100=$\frac{m}{8}$,
即m=800,
故y=$\frac{800}{x}$,
当y=20时,20=$\frac{800}{t}$,
解得:t=40;
(3)∵45-40=5≤8,
∴当x=5时,y=10×5+20=70,
答:小明散步45分钟回到家时,饮水机内的温度约为70℃.
点评 此题主要考查了一次函数以及反比例函数的应用,根据题意得出正确的函数解析式是解题关键.

练习册系列答案
相关题目
6.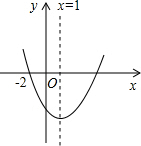 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为(4,0);③a+c>b;④若(-1,y1),($\frac{7}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的结论有( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为(4,0);③a+c>b;④若(-1,y1),($\frac{7}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的结论有( )
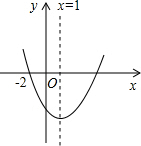 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为(4,0);③a+c>b;④若(-1,y1),($\frac{7}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的结论有( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b+2a=0;②抛物线与x轴的另一个交点为(4,0);③a+c>b;④若(-1,y1),($\frac{7}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.若一组数据1,2,3,7,x的平均数是3,则这组数的众数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 7 |
 如图,已知a∥b,∠1=48°,则∠2=132°.
如图,已知a∥b,∠1=48°,则∠2=132°.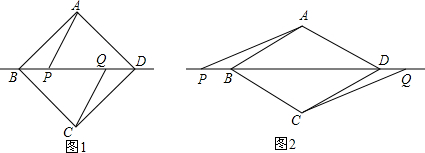
 如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).