题目内容
4. 如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).(1)①作出与△ABC关于x轴对称的△A1B1C1;
②以原点O为位似中心,在原点的另一侧画出△A2B2C2,使$\frac{AB}{{{A}_{2}B}_{2}}$=$\frac{1}{2}$.
(2)判断△A2B2C2的形状,并说明理由.
分析 (1)①利用关于x轴对称点的性质得出对应点位置进而得出答案;
②利用位似图形的性质得出关于原点位似的图形的顶点进而得出答案;
(2)利用勾股定理逆定理进而得出△A2B2C2的形状.
解答  解:(1)①如图,△A1B1C1是所求;
解:(1)①如图,△A1B1C1是所求;
②如图中△A2B2C2是所求;
(2)△A2B2C2是等腰直角三形.
理由:
∵A2B22=62+22=40,
A2C22=42+22=20,
B2C22=42+22=20,
∴A2B22=A2C22+B2C22,
故△A2B2C2是等腰直角三形.
点评 此题主要考查了轴对称变换以及位似变换和勾股定理的逆定理,得出对应点位置是解题关键.

练习册系列答案
相关题目
4.下列运算正确的是( )
| A. | a6÷a2=a3 | B. | (a+b)2=a2+b2 | C. | 2-3=-6 | D. | $\root{3}{-27}$=-3 |
19.已知m,n是方程x2+2x-5=0的两个实数根,则m2-mn+3m+n=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
9.$\sqrt{3}$sin60°的值等于( )
| A. | 1 | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{2}$ |
14.已知二次函数y=ax2+bx+c中的x,y满足下表:
根据表中信息,下列判断不正确的是( )
| X | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | … |
| A. | 开口向上 | B. | 当-1<x<2时,y<0 | ||
| C. | 图象的对称轴是直线x=$\frac{1}{2}$ | D. | 函数最小值是-2 |
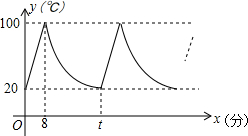 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题: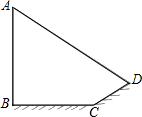 已知电线杆AB直立于地面,它的影子恰好照在土坡的坡面CD和地面BC上.如果CD与地面成45°,∠A=60°,CD=4$\sqrt{2}$米,BC=(4$\sqrt{3}$-4)米,求电线杆AB的长.
已知电线杆AB直立于地面,它的影子恰好照在土坡的坡面CD和地面BC上.如果CD与地面成45°,∠A=60°,CD=4$\sqrt{2}$米,BC=(4$\sqrt{3}$-4)米,求电线杆AB的长.