题目内容
2．
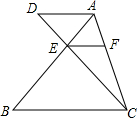如图，AD∥FE∥CB．试探究S△ADC，S△AEC，S△ABC之间的关系，并证明结论．
分析 平行线之间的距离处处相等，然后依据三角形的面积公式可得到它们的面积比等于AD、EF、BC的长度比．
解答 解：S△ADC：S△AEC：S△ABC=AD：EF：BC．
理由：如图所示：过点A作AG⊥BC，垂足为G，交EF于点O，过点C作CH⊥AD，垂足为H．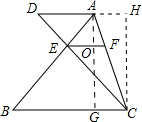
∵AD∥FE∥CB，
∴AG=CH．
∴${S}_{ADC}=\frac{1}{2}AD•CH$，．S△AEC=S△AEF+S△EFC=$\frac{1}{2}EF•AG$，${S}_{△ABC}=\frac{1}{2}BC•AG$．
∴S△ADC：S△AEC：S△ABC=AD：EF：BC．
点评 本题主要考查的是平行线之间的距离、三角形的面积公式，明确平行线之间的距离处处相等是解题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
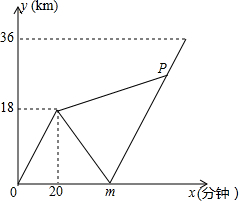甲、乙两名大学生去距学校36千米的某乡镇进行社会调查，他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车前往，乙骑电动车按原路返回，乙取相机后（在学校取相机所用时间忽略不计）骑电动车追甲．在距乡镇13.5千米处追上甲后同车前往乡镇．乙电动车的速度始终不变．设甲与学校相距y甲（千米），乙与学校相离y乙（千米），甲离开学校的时间为x（分钟）．y甲、y乙与x之间的函数图象如图所示，结合图象解答下列问题：