题目内容
7. 如图所示,点B,E,F,C在同一条直线上,AF⊥BC于F,DE⊥BC于E,AB∥CD,BE=CF,求证:AB=DC.
如图所示,点B,E,F,C在同一条直线上,AF⊥BC于F,DE⊥BC于E,AB∥CD,BE=CF,求证:AB=DC.
分析 根据全等三角形的判断和性质即可得到结论.
解答 证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
∵AB∥CD,
∴∠B=∠C,
∵AF⊥BC于F,DE⊥BC于E,
∴∠AFB=∠DEC=90°,
在△ABF与△DCE中$\left\{\begin{array}{l}{∠B=∠C}\\{BF=CE}\\{∠AFB=∠DEC}\end{array}\right.$,
∴△ABF≌△DEC,
∴AB=DC.
点评 本题考查了全等三角形的判断和性质,平行线的性质,熟练掌握全等三角形的判断和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.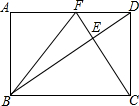 如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )
如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )
 如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )
如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
17.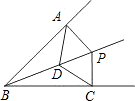 如图,己知点P在射线BD上,PA⊥AB,PC⊥BC,垂足分别为A,C,且PA=PC,下列结论错误的是( )
如图,己知点P在射线BD上,PA⊥AB,PC⊥BC,垂足分别为A,C,且PA=PC,下列结论错误的是( )
 如图,己知点P在射线BD上,PA⊥AB,PC⊥BC,垂足分别为A,C,且PA=PC,下列结论错误的是( )
如图,己知点P在射线BD上,PA⊥AB,PC⊥BC,垂足分别为A,C,且PA=PC,下列结论错误的是( )| A. | AD=CP | B. | 点D在∠ABC的平分线上 | ||
| C. | △ABD≌△CBD | D. | ∠ADB=∠CDB |
 如图,两条平行的公路AB与CD之间有一个斜坡AC,在C处垂直树立着一个路灯CE,灯杆CE上有两根灯臂EF和EG,两灯臂上的路灯F、G分别照明AB、CD两条公路.已知AC=CE=2米,EG=1米,∠BAC=120°,∠FEG=135°.EF∥AB,分别求路灯F到公路AB、路灯G到公路CD的距离(结果精确到0.1米.参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
如图,两条平行的公路AB与CD之间有一个斜坡AC,在C处垂直树立着一个路灯CE,灯杆CE上有两根灯臂EF和EG,两灯臂上的路灯F、G分别照明AB、CD两条公路.已知AC=CE=2米,EG=1米,∠BAC=120°,∠FEG=135°.EF∥AB,分别求路灯F到公路AB、路灯G到公路CD的距离(结果精确到0.1米.参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).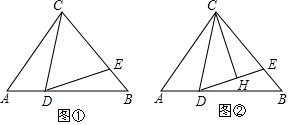
 如图,AC、BC分别平分∠MAB和∠ABN,∠ACB=90°.
如图,AC、BC分别平分∠MAB和∠ABN,∠ACB=90°.