题目内容
5．已知$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{5}$，则$\frac{x+y-z}{x+y+z}$的值为$\frac{1}{6}$．分析 根据等式的性质，可用k表示x，y，z，根据等式的性质，可得答案．
解答 解：设$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{5}$=k，得x=3k，y=4k，z=5k．
$\frac{x+y-z}{x+y+z}$=$\frac{3k+4k-5k}{3k+4k+5k}$=$\frac{1}{6}$，
故答案为：$\frac{1}{6}$．
点评 本题考查了比例的性质，利用等式的性质得出x=3k，y=4k，z=5k是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．
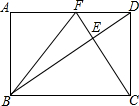如图，在矩形ABCD中，DC=2$\sqrt{3}$，CF⊥BD分别交BD、AD于点E、F，连接BF．当F为AD的中点时，则BC的长为（ ）
如图，在矩形ABCD中，DC=2$\sqrt{3}$，CF⊥BD分别交BD、AD于点E、F，连接BF．当F为AD的中点时，则BC的长为（ ）| A． | 4 | B． | 3$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 2$\sqrt{6}$ |
10．已知$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{11x-13y=15}\\{7x+9y=-25}\end{array}\right.$的解，则下列说法中正确的是（ ）
| A． | $\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程11x-13y=15的唯一一组解 | |
| B． | $\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程7x+9y=-25的唯一一组解 | |
| C． | x=a是方程x+5=0的解 | |
| D． | y=b是方程y-6=-8的解 |
17．
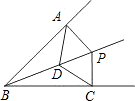如图，己知点P在射线BD上，PA⊥AB，PC⊥BC，垂足分别为A，C，且PA=PC，下列结论错误的是（ ）
如图，己知点P在射线BD上，PA⊥AB，PC⊥BC，垂足分别为A，C，且PA=PC，下列结论错误的是（ ）| A． | AD=CP | B． | 点D在∠ABC的平分线上 | ||
| C． | △ABD≌△CBD | D． | ∠ADB=∠CDB |