题目内容
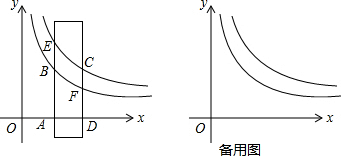
6.在平面直角坐标系xOy中,有一宽为1的长方形纸带,平行于y轴,在x轴的正半轴上移动,交x轴的正半轴于点A,D,两边分别交函数y1=$\frac{2}{x}$(x>0)与y2=$\frac{3}{x}$(x>0)的图象于B、F和E、C(如图),设点A的横坐标为m.(1)连接OB,OE,求△OBE的面积;
(2)连接BC,当m为何值时,四边形ABCD是矩形;
(3)在纸带在平移的过程中,能否使点O、B、C三点在同一直线上?若能,求出此时m的值;若不能,试说明理由.
分析 (1)利用反比例函数k的几何意义可求得S△OAB和S△OAE,则可求得S△OBE;
(2)用m可表示出B、C的坐标,由矩形的性质可知AB∥CD且AB=CD,可得到关于m的方程,可求得m的值;
(3)用m可表示出B、C的坐标,则可表示出OA、OD、AB和CD的长,当O、B、C三点在一条线上时,利用平行线分线段成比例的性质可得到关于m的方程,可求得m的值.
解答 解:
(1)如图1,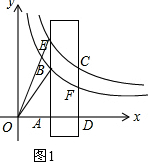
∵点B在y1=$\frac{2}{x}$(x>0)的图象上,
∴OA•AB=2,
同理OA•AE=3,
∴S△OBE=S△OAE-S△OAB=$\frac{1}{2}$OA•AE-$\frac{1}{2}$OA•AB=$\frac{3}{2}$-1=$\frac{1}{2}$;
(2)∵点B在y1=$\frac{2}{x}$(x>0)的图象上,且OA=m,
∴AB=$\frac{2}{m}$,OD=OA+AD=m+1,
∵点C在y2=$\frac{3}{x}$(x>0)的图象上,
∴CD=$\frac{3}{m+1}$,
当四边形ABCD为矩形时,则AB=CD,
∴$\frac{2}{m}$=$\frac{3}{m+1}$,解得m=2,经检验m=2是原方程的解,
∴当m的值为2时,四边形ABCD为矩形;
(3)如图2,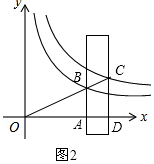
由(2)可知OA=m,OD=m+1,AB=$\frac{2}{m}$,CD=$\frac{3}{m+1}$,
∵O、B、C三点在一条线上,且AB∥CD,
∴$\frac{OA}{OD}$=$\frac{AB}{CD}$,即$\frac{m}{m+1}$=$\frac{\frac{2}{m}}{\frac{3}{m+1}}$,解得m=2+$\sqrt{5}$或m=2-$\sqrt{5}$(舍去),
∴当m的值为2+$\sqrt{5}$时,O、B、C三点在一条线上.
点评 本题为反比例函数的综合应用,涉及反比例函数k的几何意义、三角形的面积、矩形的性质、平行线分线段成比例等知识.在(1)中掌握好反比例函数中k的几何意义是解题的关键,在(2)中利用矩形的性质得到关于m的方程是解题的关键,在(3)中利用平行线分线段成比例是解题的关键.本题考查知识点较多,综合性较强,难度适中.

(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
| 粗加工数量/吨 | 3 | 7 | x |
| 精加工数量/吨 | 47 | 43 | 50-x |
| 粗加工数量/吨 | 3 | 7 | x |
| 粗加工获利/元 | 1200 | 2800 | 400x |
| 精加工获利/元 | 28200 | 25800 | 600(50-x) |
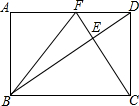 如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )
如图,在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.当F为AD的中点时,则BC的长为( )| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
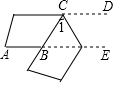 如图,将CD翻折至CB位置,已知AB∥CD,∠CBE=70°,则∠1的度数是55°.
如图,将CD翻折至CB位置,已知AB∥CD,∠CBE=70°,则∠1的度数是55°.
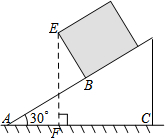 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,己知木箱高BE=$\sqrt{3}$m,斜面坡角为30°,则木箱端点E距地面AC的高度为3m.
一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,己知木箱高BE=$\sqrt{3}$m,斜面坡角为30°,则木箱端点E距地面AC的高度为3m.