题目内容
15.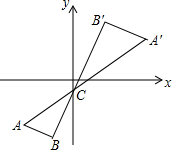 如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).
如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).
分析 作AF⊥y轴于F,A′E⊥y轴于E,根据题意求出A′E和EC的长,根据相似三角形的性质求出AF和CF的长,确定点A的坐标.
解答 解: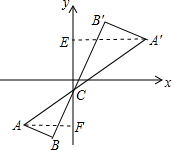 作AF⊥y轴于F,A′E⊥y轴于E,
作AF⊥y轴于F,A′E⊥y轴于E,
∵点A′的坐标为(a,b),
∴A′E=a,EC=b+1,
由题意得,△A′B′C′和△ABC的相似比是1:2,
∴$\frac{AF}{A′E}$=$\frac{CF}{CE}$=$\frac{1}{2}$,
∴AF=$\frac{1}{2}$a,CF=$\frac{1}{2}$(b+1),
∴点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).
故答案为:(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).
点评 本题考查的是位似变换和坐标与图形的性质,掌握位似是相似的特殊形式,位似比等于相似比是解题的关键,注意点的坐标的确定与象限的关系要明确.

练习册系列答案
相关题目
6.若|X|=3,|Y|=4,且X<Y,那么X+Y=( )
| A. | +1或+7 | B. | -1或-7 | C. | +1或-7 | D. | -1或+7 |
4.a为任意实数,一次函数y=ax-2a+1的图象必过一定点,此顶点的坐标为( )
| A. | (0,1) | B. | (1,2) | C. | (2,1) | D. | (2,0) |
 如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.
如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6. 如图:抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m与直线y2=2x-4交于x轴上A点和另一点B.
如图:抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m与直线y2=2x-4交于x轴上A点和另一点B.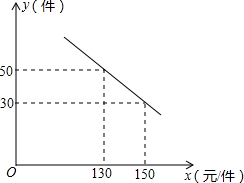 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: