题目内容
5. 如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.
如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.
分析 延长AM、PB交于点C,过点M作MH⊥AB于H,取AB的中点N,连接MN,易证△APM≌△CPM,则有AM=CM,PA=PC,由PA-PB=4可得BC=2,根据三角形中位线定理可得MN=2,根据点到直线之间垂线段最短可得MH≤2,从而可求出△AMB的面积的最大值.
解答 解:延长AM、PB交于点C,过点M作MH⊥AB于H,取AB的中点N,连接MN,如图.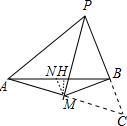
∵PM平分∠APB,AM⊥PM,
∴∠APM=∠CPM,∠AMP=∠CMP=90°.
在△APM和△CPM中,
$\left\{\begin{array}{l}{∠APM=∠CPM}\\{PM=PM}\\{∠AMP=∠CMP}\end{array}\right.$,
∴△APM≌△CPM,
∴AM=CM,PA=PC.
∵PA-PB=4,
∴BC=PC-PB=PA-PB=4.
∵AM=CM,AN=BN,
∴MN=$\frac{1}{2}$BC=2.
∵MH⊥AB,
∴MH≤2.
当BC⊥AB时,MN与MH重合,此时,MH取得最大值2,
△AMB的面积也就取到最大值,最大值为6.
故答案为6.
点评 本题主要考查了全等三角形的判定与性质、三角形中位线定理、点到直线之间垂线段最短等知识,由角的一边的点向角平分线作垂线段想到补全全等三角形是解决本题的关键.

练习册系列答案
相关题目
10.$\sqrt{{x^2}-4x+4}$=x-2,则( )
| A. | x>-2 | B. | x≥2 | C. | x<-2 | D. | x≥-2 |
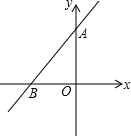 直线y=x+3与x轴,y轴交于点A、B,求:
直线y=x+3与x轴,y轴交于点A、B,求: 如图,在△ABC中,AD、AE分别是边BC上的中线和高,AE=2cm,S△ABC=6cm2,求DC的长.
如图,在△ABC中,AD、AE分别是边BC上的中线和高,AE=2cm,S△ABC=6cm2,求DC的长.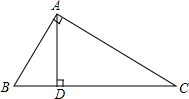 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.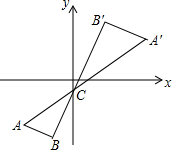 如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).
如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).