题目内容
2.已知:正方形ABCD.(1)如图①,E,F分别是边CD,AD上的一点,且AE⊥BF,求证:AE=BF.
(2)M,N,E,F分别在边AB,CD,AD,BC上,且MN=EF,那么MN⊥EF?请画图表示,并作简要说明:
(3)如图④,将正方形ABCD折叠,使得点A落在边CD上的E点,折痕为MN,若已知该正方形边长为12,MN的长为13,求CE的长.
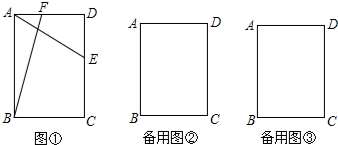
分析 (1)由正方形的性质得出AB=AD,∠BAF=∠ADE=90°,证出∠ABF=∠DAE,由ASA证明△BAF≌△ADE,得出对应边相等即可;
(2)过点E作EG⊥BC于点G,过点M作MP⊥CD于点P,设EF与MN相交于点O,MP与EF相交于点Q,由正方形的性质可得EG=MP,先利用“HL”证明Rt△EFG≌Rt△MNP,由全等三角形对应角相等可得∠MNP=∠EFG,再由角的关系推出∠EQM=∠MNP,由∠MNP+∠NMP=90°得出∠NMP+∠EQM=90°,得出∠MOQ=90°,由垂直的定义得出MN⊥EF,当E向D移动,F向B移动,同样使MN=EF,此时就不垂直;
(3)连接AE时,则线段MN垂直平分AE,过点B作BF∥MN,则BF=MN,且AE⊥BF,由(1)知AE=BF=MN=13,由勾股定理求出DE,即可得出CE的长.
解答 (1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAF=∠ADE=90°,
∵AE⊥BF,
∴∠BAE+∠ABF=90°,
∵∠BAE+∠DAE=90°,
∴∠ABF=∠DAE,
在△BAF和△ADE中,
$\left\{\begin{array}{l}{∠ABF=∠DAE}\\{AD=AB}\\{∠ADE=∠BAF}\end{array}\right.$,
∴△BAF≌△ADE(ASA),
∴AE=BF;
(2)解:MN与EF不一定垂直; 如图1所示,当MN=EF时,MN⊥EF,
如图1所示,当MN=EF时,MN⊥EF,
如图2所示,当MN=EF时,MN与EF就不垂直了;
理由如下:过点E作EG⊥BC于点G,过点M作MP⊥CD于点P,
设EF与MN相交于点O,MP与EF相交于点Q,
∵四边形ABCD是正方形,
∴EG=MP, 在Rt△EFG和Rt△MNP中,
在Rt△EFG和Rt△MNP中,
$\left\{\begin{array}{l}{MN=EF}\\{EG=MP}\end{array}\right.$,
∴Rt△EFG≌Rt△MNP(HL),
∴∠MNP=∠EFG,
∵MP⊥CD,∠C=90°,
∴MP∥BC,
∴∠EQM=∠EFG=∠MNP,
又∵∠MNP+∠NMP=90°,
∴∠EQM+∠NMP=90°,
在△MOQ中,∠MOQ=180°-(∠EQM+∠NMP)=180°-90°=90°,
∴MN⊥EF,
当E向D移动,F向B移动,同样使MN=EF,此时就不垂直,
故此,MN与EF不一定垂直;
(3)解:如图3所示,连接AE,
则线段MN垂直平分AE,
过点B作BF∥MN,
则四边形MNBF是平行四边形,
∴BF=MN,且AE⊥BF,
由(1)知AE=BF=MN=13,
由勾股定理得:DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴CE=CD-DE=12-5=7.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、勾股定理、平行四边形的判定与性质等知识;本题难度较大,综合性强.

 巧学巧练系列答案
巧学巧练系列答案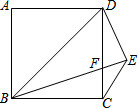 如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )
如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
| A. | -$\sqrt{3}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | |-2| |
 如图,△ABC的点A的坐标是(3,4),点B的坐标是(1,2).
如图,△ABC的点A的坐标是(3,4),点B的坐标是(1,2).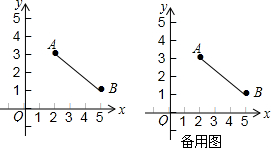
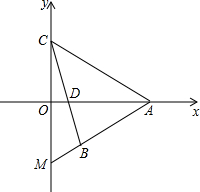 一次函数y=kx-4k交x轴正半轴于点A,交y轴正半轴于点C,当k变化时,作点C关于x轴对称的点M,CB交AM于B,交x轴于D,且2∠OCD=∠CAO,求AB+AC的值.
一次函数y=kx-4k交x轴正半轴于点A,交y轴正半轴于点C,当k变化时,作点C关于x轴对称的点M,CB交AM于B,交x轴于D,且2∠OCD=∠CAO,求AB+AC的值.