题目内容
11.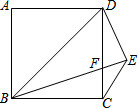 如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )
如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
分析 把△BCE逆时针旋转90°得到△BAG,连接DG、AC、AG;则∠BAG=∠BCE,BG=BE,∠GBE=90°,先证出C、A、G三点共线,得出∠DAG135°,∠BAG=∠DAG,由SAS证明△BAG≌△DAG,得出BG=DG,证出BG=DG=BE,即△BDG是等边三角形,得出∠GBD=60°,∠DBE=30°,再由三角形的外角性质求出∠DFE即可.
解答 解:把△BCE逆时针旋转90°得到△BAG,连接DG、AC、AG;如图所示: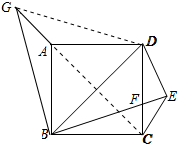
则∠BAG=∠BCE,BG=BE,∠GBE=90°,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠BAC=∠DAC=∠BDC=45°,AB=AD,
∵CE∥BD,
∴∠DCE=∠BDC=45°,
∴∠BCE=90°+45°=135°,
∴∠BAG=135°,
∴∠BAG=135°,
∴∠BAG+∠BAC=135°+45°=180°,
∴点C、A、G三点共线,
∴∠DAG=180°-45°=135°,
∴∠BAG=∠DAG,
在△BAG和△DAG中,
$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAG=∠DAG}&{\;}\\{AG=AG}&{\;}\end{array}\right.$,
∴△BAG≌△DAG(SAS),
∴BG=DG,
∵BD=BE,
∴BG=DG=BE,
即△BDG是等边三角形,
∴∠GBD=60°,
∴∠DBE=90°-60°=30°,
∴∠DFE=∠DBE+∠BDC=°+45°=75°.
故选:C.
点评 本题考查了正方形的性质、全等三角形的判定与性质、三点共线、等边三角形的判定与性质、三角形的外角性质;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
19.若一个三角形有两条边长分别为2和8,且周长为奇数,则第三条边的长度为( )
| A. | 7 | B. | 9 | C. | 17或19 | D. | 7或9 |
6.一辆加满汽油的汽车在匀速行驶中,油箱中的剩余油量Q(1)与行驶的时间t(h)的关系如下表所示:
请你根据表格,解答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)随着行驶的时间的不断增加,油箱中的剩余油量的变化趋势是怎样的?
(3)请直接写出Q与t的关系式,并求出这辆汽车在连续行驶6h后,油箱中的剩余油量;
(4)这辆车在中途不加油的情况下,最多能连续行驶的时间是多少?
| 行驶时间t(h) | 0 | 1 | 2 | 3 | 4 | … |
| 油箱中的剩余油量Q(1) | 54 | 46.5 | 39 | 31.5 | 24 | … |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)随着行驶的时间的不断增加,油箱中的剩余油量的变化趋势是怎样的?
(3)请直接写出Q与t的关系式,并求出这辆汽车在连续行驶6h后,油箱中的剩余油量;
(4)这辆车在中途不加油的情况下,最多能连续行驶的时间是多少?
16. 已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
 已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
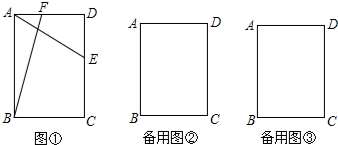
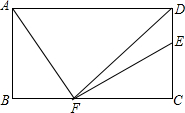 如图,矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.
如图,矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF. 如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=4:1,那么∠AOC的度数是72°.
如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=4:1,那么∠AOC的度数是72°.