题目内容
7.平面直角坐标系xOy中平行四边形ABCD,其中顶点A、B坐标分别为(2,3)、(5,1).(1)若点C在x轴正半轴上,点D在y轴正半轴上,写出顶点C和D的坐标;
(2)若(1)条件改为点C、D在坐标轴上,写出点C、D的坐标.
分析 (1)如图1,过点A作AM⊥y轴于M,过点B作BN⊥x轴于N,连接AC,证得△AMD≌△BCN,于是得到AM=CN=2,MD=BN=1,求得OD=2,OC=3,于是得到结论;
(2)如图2,点C、D在坐标轴上,四边形ABCD是平行四边形,得到线段C′D′与DC关于原点对称,即可得到结果.
解答 解:(1)如图1,过点A作AM⊥y轴于M,过点B作BN⊥x轴于N,连接AC,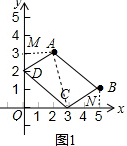
∴∠MAC=∠ACN,
∵AD∥BC,∴∠DAC=∠ACB,
∴∠MAD=∠BCN,
在△AMD与△BCN中,
$\left\{\begin{array}{l}{∠AMD=∠BNC=90°}\\{∠MAD=∠BCN}\\{AD=BC}\end{array}\right.$,
∴△AMD≌△BCN,
∴AM=CN=2,MD=BN=1,
∴OD=2,OC=3,
∴C(3,0),D(0,2);
(2)如图2,点C、D在坐标轴上,四边形ABCD是平行四边形,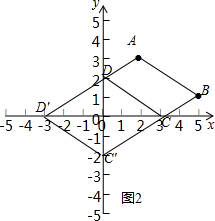
∴除(1)中求出的C,D之外,还有一组C′,D′,线段C′D′与DC关于原点对称,
∴C′(0,-2),D′(-3,0).
点评 本题考查了平行四边形的性质,坐标与图形的性质,全等三角形的判定和性质,熟练掌握平行四边形的性质定理是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.将边长为1的正方形,按如图所示的方式分割,第1次分割后的阴影部分面积S1=$\frac{1}{2}$,第2次分割后的阴影部分面积S2=$\frac{3}{4}$,第3次分割后的阴影部分面S3=$\frac{7}{8}$,…,按照这样的规律分割,则第n(n为正整数)次分割后的阴影部分面积可用n表示为Sn=( )


| A. | $\frac{1}{{2}^{n}}$ | B. | 1-$\frac{1}{{2}^{n}}$ | C. | 1-$\frac{1}{{2}^{n+1}}$ | D. | 1-$\frac{1}{{2}^{n-1}}$ |
19.若一个三角形有两条边长分别为2和8,且周长为奇数,则第三条边的长度为( )
| A. | 7 | B. | 9 | C. | 17或19 | D. | 7或9 |
16. 已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
 已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )| A. | 20 | B. | 16 | C. | 12 | D. | 10 |