题目内容
3.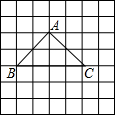 如图,△ABC的点A的坐标是(3,4),点B的坐标是(1,2).
如图,△ABC的点A的坐标是(3,4),点B的坐标是(1,2).(1)请写出点C的坐标(5,2);
(2)将△ABC向下平移一个单位得到△A1B1C1,请你画出△A1B1C1,并写出点A1的坐标(3,3);
(3)△A1B1C1与△ABC是否有重合部分?如果有,请你求出重合部分的面积.
分析 (1)根据A(3,4),B(1,2)建立坐标系,写出C点坐标即可;
(2)根据图形平移的性质画出△A1B1C1即可;
(3)根据三角形的面积公式即可得出结论.
解答  解:(1)由图可知,C(5,2).
解:(1)由图可知,C(5,2).
故答案为:( 5,2);
(2)由图可知,A1(3,3).
故答案为:(3,3);
(3)由图可知,S△=$\frac{1}{2}$×2×1=1.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
13.下列分式中,是最简分式的是( )
| A. | $\frac{2a}{3{a}^{2}b}$ | B. | $\frac{x+y}{{x}^{2}+{y}^{2}}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{{a}^{2}+ab}{ab+{b}^{2}}$ |
8.将边长为1的正方形,按如图所示的方式分割,第1次分割后的阴影部分面积S1=$\frac{1}{2}$,第2次分割后的阴影部分面积S2=$\frac{3}{4}$,第3次分割后的阴影部分面S3=$\frac{7}{8}$,…,按照这样的规律分割,则第n(n为正整数)次分割后的阴影部分面积可用n表示为Sn=( )


| A. | $\frac{1}{{2}^{n}}$ | B. | 1-$\frac{1}{{2}^{n}}$ | C. | 1-$\frac{1}{{2}^{n+1}}$ | D. | 1-$\frac{1}{{2}^{n-1}}$ |
15.已知甲、乙、丙三个数,甲=5+$\sqrt{13}$,乙=2+$\sqrt{19}$,且甲>丙>乙,则下列符合条件的丙是( )
| A. | 1+$\sqrt{23}$ | B. | 4+$\sqrt{26}$ | C. | 4+$\sqrt{15}$ | D. | 4+$\sqrt{3}$ |
 计算或化简求值.
计算或化简求值.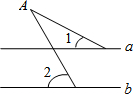 如图,已知直线a∥b,∠1=28°,∠2=52°,那么∠A的度数是24°.
如图,已知直线a∥b,∠1=28°,∠2=52°,那么∠A的度数是24°.