题目内容
14.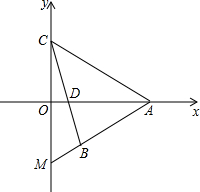 一次函数y=kx-4k交x轴正半轴于点A,交y轴正半轴于点C,当k变化时,作点C关于x轴对称的点M,CB交AM于B,交x轴于D,且2∠OCD=∠CAO,求AB+AC的值.
一次函数y=kx-4k交x轴正半轴于点A,交y轴正半轴于点C,当k变化时,作点C关于x轴对称的点M,CB交AM于B,交x轴于D,且2∠OCD=∠CAO,求AB+AC的值.
分析 作∠OAC的平分线AE,作EF⊥AC于F,根据勾股定理求得AC,根据角平分线的性质求得AF=OA=4,EF=EO,从而求得CF=4$\sqrt{1+{k}^{2}}$-4,在RT△CEF中,根据勾股定理求得CE=$\frac{4}{k}$[$\sqrt{1+{k}^{2}}$-($\sqrt{1+{k}^{2}}$)2],然后根据△CMB∽△ACE,对应边成比例求得BM=-8(1-$\sqrt{1+{k}^{2}}$),则AB+AC=2AC-BM=8.
解答  解:作∠OAC的平分线AE,作EF⊥AC于F,
解:作∠OAC的平分线AE,作EF⊥AC于F,
由一次函数y=kx-4k可知,A(4,0),C(0,-4k),
∴AC=$\sqrt{{4}^{2}+(4k)^{2}}$=4$\sqrt{1+{k}^{2}}$,
由角平分线的性质可知:AF=OA=4,EF=EO,
∴CF=4$\sqrt{1+{k}^{2}}$-4,
设CE=x,则EF=OE=-4k-x,
∵CE2=CF2+EF2
∴x2=(4$\sqrt{1+{k}^{2}}$-4)2+(-4k-x)2,
解得x=$\frac{4}{k}$[$\sqrt{1+{k}^{2}}$-($\sqrt{1+{k}^{2}}$)2],
∴CE=$\frac{4}{k}$[$\sqrt{1+{k}^{2}}$-($\sqrt{1+{k}^{2}}$)2],
∵∠CAE=∠OCD,∠ACE=∠CMB,
∴△CMB∽△ACE,
∴$\frac{BM}{CE}$=$\frac{CM}{AC}$,
∵点M是点C关于x轴对称的点,
∴CM=-4k×2=-8k,
即$\frac{BM}{\frac{4}{k}[\sqrt{1+{k}^{2}}-(\sqrt{1+{k}^{2}})^{2}]}$=$\frac{-8k}{4\sqrt{1+{k}^{2}}}$,
∴BM=-8(1-$\sqrt{1+{k}^{2}}$),
∴AB+AC=2AC-BM=2×4$\sqrt{1+{k}^{2}}$+8(1-$\sqrt{1+{k}^{2}}$)=8.
点评 本题是一次函数的综合题,考查了轴对称的性质,角平分线的性质,勾股定理的应用,三角形相似的判定和性质等,熟练掌握性质定理是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 1+$\sqrt{23}$ | B. | 4+$\sqrt{26}$ | C. | 4+$\sqrt{15}$ | D. | 4+$\sqrt{3}$ |
| A. | 7 | B. | 9 | C. | 17或19 | D. | 7或9 |
| 行驶时间t(h) | 0 | 1 | 2 | 3 | 4 | … |
| 油箱中的剩余油量Q(1) | 54 | 46.5 | 39 | 31.5 | 24 | … |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)随着行驶的时间的不断增加,油箱中的剩余油量的变化趋势是怎样的?
(3)请直接写出Q与t的关系式,并求出这辆汽车在连续行驶6h后,油箱中的剩余油量;
(4)这辆车在中途不加油的情况下,最多能连续行驶的时间是多少?
 在平面直角坐标系中,点P从原点O出发,且点P只能每次向上平移2个单位长度或向右平移1个单位长度.
在平面直角坐标系中,点P从原点O出发,且点P只能每次向上平移2个单位长度或向右平移1个单位长度.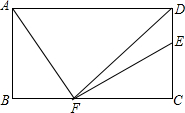 如图,矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.
如图,矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.