题目内容
1.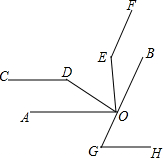 已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.
已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.(1)除∠E外在图中还能找出与∠D相等的角吗?为什么?
(2)若∠D-∠G=90°,问CD与GH平行吗?为什么?
分析 (1)由平行线的性质和邻补角定义得出∠E=∠EOG,由∠D=∠E,即可得出∠EOG=∠D;
(2)先求出∠AOD=∠BOE,再证出∠D+∠AOD=180°,得出CD∥AO,证出∠AOG=∠D-90°,得出∠G=∠AOG,证出AO∥GH,即可得出结论.
解答 解:(1)∠EOG=∠D;理由如下:
∵EF∥BG,
∴∠E+∠BOE=180°,
∵∠BOE+∠EOG=180°,
∴∠E=∠EOG,
∵∠D=∠E,
∴∠EOG=∠D;
(2)CD∥GH;理由如下:
∵∠AOE=∠BOD=90°,
∴∠AOD=∠BOE,
∵∠E+∠BOE=180°,∠D=∠E,
∴∠D+∠AOD=180°,
∴CD∥AO,
∵∠AOG=90°-(180°-∠D)=∠D-90°,
∵∠D-∠G=90°,
∴∠G=∠AOG,
∴AO∥GH,
∴CD∥GH.
点评 本题考查了平行线的判定与性质、邻补角定义;熟练掌握平行线的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
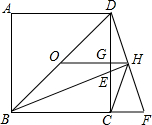 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中正确结论的个数为( )
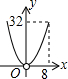
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中正确结论的个数为( )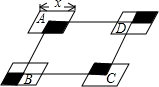 如图,平行四边形ABCD的边长AD为8,面积为32,四个全等的小平行四边形对称中心分别在平行四边形ABCD的顶点上,它们的各边与平行四边形ABCD的各边分别平行,且与平行四边形ABCD相似.若平行四边形的一边长为x,且0<x≤8,阴影部分的面积和为y,则y与x之间的函数关系的大致图象是( )
如图,平行四边形ABCD的边长AD为8,面积为32,四个全等的小平行四边形对称中心分别在平行四边形ABCD的顶点上,它们的各边与平行四边形ABCD的各边分别平行,且与平行四边形ABCD相似.若平行四边形的一边长为x,且0<x≤8,阴影部分的面积和为y,则y与x之间的函数关系的大致图象是( )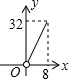
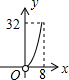
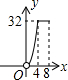
 如图所示,问∠1,∠2,∠3,∠4要满足什么条件可以证明AB∥CD?
如图所示,问∠1,∠2,∠3,∠4要满足什么条件可以证明AB∥CD? 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题: