题目内容
11. 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:(1)根据图象,轮船比快艇早出发2小时.
(2)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围);
(3)通过计算说明快艇出发多长时间赶上轮船?
分析 (1)由图象即可得解;
(2)可根据图中给出的信息,用待定系数法分别求出轮船与快艇的函数关系式.
(3)当快艇追上轮船时两者走的路程相同,根据(1)求出的函数式,让两者的路程相等,即可得出时间的值.
解答 解:(1)根据图象,轮船比快艇早出发2小时,
故答案为2;
(2)设表示轮船行驶过程的函数式为y=kx.由图象知:
当x=8时,y=160.
∴8k=160,解得:k=20.
∴表示轮船行驶过程的函数式为y=20x.
设表示快艇行驶过程的函数解析式为y=ax+b.
由图象知:当x=2时,y=0;当x=6时,y=160
∴$\left\{\begin{array}{l}{2a+b=0}\\{6a+b=160}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=40}\\{b=-80}\end{array}\right.$.
因此表示快艇行驶过程的函数解析式为y=40x-80;
(3)设轮船出发x小时后快艇追上轮船.
20x=40x-80,
x=4,
则x-2=2.
答:快艇出发2小时后赶上轮船.
点评 本题考查了一次函数的图象的运用,行程问题的数量关系的运用,解答时分析清楚函数图象提供的信息是关键.

练习册系列答案
相关题目
16.已知一个两位数,其个位上的数为x,十位上的数比个位上的数大1,则这个两位数可表示为( )
| A. | 11x-1 | B. | 11x-10 | C. | 11x+1 | D. | 11x+10 |
20.寒假期间,九(1)班n名同学为了相互表达春节的祝愿,约定每两名同学之间互发一次信息,那么互发信息的总次数m与n的函数关系式可以表示为( )
| A. | m=$\frac{1}{2}$n(n+1) | B. | m=$\frac{1}{2}$n(n-1) | C. | m=$\frac{1}{2}$n2 | D. | m=n(n-1) |
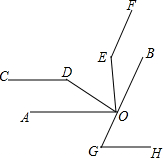 已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.
已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E. 如图,在△ABC中,AD是高,AE是角平分线,∠B=70°,∠DAE=18°,求∠C的度数.
如图,在△ABC中,AD是高,AE是角平分线,∠B=70°,∠DAE=18°,求∠C的度数.