题目内容
9.已知$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax+cy=1}\\{cx-by=2}\end{array}\right.$的解,(1)求a,b间的关系;
(2)求52•5a•252b的值.
分析 (1)首先将方程的解代入得到关于a、b、c的方程组,然后消取字母参数c即可;
(2)首先利用同底数幂的乘法法则计算,然后将a+2b的值代入计算即可.
解答 解:(1)将$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$代入方程得:-a-2c=1①,-c+b=2②.
由②得;c=b-2③,将③代入①得:-a-2(b-2)=1.
整理得:a+2b=3.
(2)52•5a•252b=52+a+2b=52+3=55=3125.
点评 本题主要考查的是方程组的解的定义、同底数幂的乘法,消去字母参数c是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
20.已知数据a1,a2,a3的平均数是$\overline{a}$,那么2a1+1,2a2+1,2a3+1的平均数是( )
| A. | $\overline{a}$ | B. | 2$\overline{a}$ | C. | 2$\overline{a}$+1 | D. | $\frac{2}{3}$$\overline{a}$+1 |
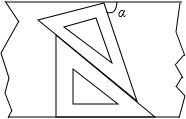 如图,一副三角板放置在两边互相平行的纸板上,其中下面部分是含45°角的三角板上,上面部分是一个含30°角的三角板,则图中∠α的度数是75°.
如图,一副三角板放置在两边互相平行的纸板上,其中下面部分是含45°角的三角板上,上面部分是一个含30°角的三角板,则图中∠α的度数是75°.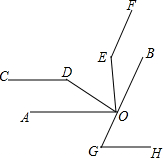 已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.
已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E. 如图,已知:AB∥CD,∠B+∠D=180°,BC与DE有何位置关系?并说明理由.
如图,已知:AB∥CD,∠B+∠D=180°,BC与DE有何位置关系?并说明理由.