题目内容
16.关于x、y的方程组$\left\{\begin{array}{l}{x-y=2m+4}\\{x+2y=1-m}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$(1)若a=0,求b的值;
(2)若点P(a,b)在y轴的右侧,求m的取值范围.
分析 (1)把x=a=0代入方程组,消去m求出y的值,即为b的值;
(2)方程组消去x表示出y,根据P在y轴右侧,得到y=b>0,即可求出m的范围.
解答 解:(1)把x=a=0代入方程组得:$\left\{\begin{array}{l}{-y=2m+4①}\\{2y=1-m②}\end{array}\right.$,
①+②×2得:3y=6,即y=2,
则b=2;
(2)方程组消去x得:3y=-3m-3,即y=-m-1,
由P(a,b)在y轴右侧,得到b>0,即y=b=-m-1>0,
解得:m<-1.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
相关题目
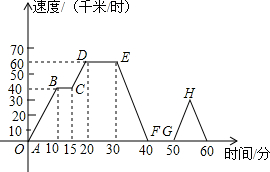 星期天到外婆家去,他记录了汽车行驶的速度随时间的变化情况,到了外婆家画出如图所示的图象
星期天到外婆家去,他记录了汽车行驶的速度随时间的变化情况,到了外婆家画出如图所示的图象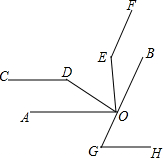 已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.
已知,点O在BC上,∠AOE=∠BOD=90°,EF∥OB,∠D=∠E.