题目内容
8.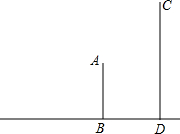 已知如图,从20米高的甲楼A望乙楼顶C处的仰角是30°,望乙楼底D处的俯角是45°,求乙楼的高度(精确到0.1米,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
已知如图,从20米高的甲楼A望乙楼顶C处的仰角是30°,望乙楼底D处的俯角是45°,求乙楼的高度(精确到0.1米,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
分析 本题是一个直角梯形的问题,可以通过点A作AE⊥CD于点E,把求CD的问题转化求CE的长.首先在Rt△ADE中求得AE的长,进而可在Rt△ACE中,利用三角函数求出CE的长.
解答  解:过点A作AE⊥CD,垂足为E,
解:过点A作AE⊥CD,垂足为E,
∵AB⊥BD,CD⊥BD,
∴四边形ABDE是矩形,
∴DE=AB=20米,
在Rt△ADE中,
∠DAE=45°,
DE=20米,
∴AE=20米,
在Rt△ACE中,CE=AE•tan30°=$\frac{20\sqrt{3}}{3}$米,
∴CD=CE+ED=$\frac{20\sqrt{3}}{3}$+20=20($\frac{\sqrt{3}}{3}$+1)≈31.5(米),
答:乙楼的高度约为31.5米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图,在△ABC中,点E、F分别是AB、AC的中点,则下列结论不正确的是( )
如图,在△ABC中,点E、F分别是AB、AC的中点,则下列结论不正确的是( )
 如图,在△ABC中,点E、F分别是AB、AC的中点,则下列结论不正确的是( )
如图,在△ABC中,点E、F分别是AB、AC的中点,则下列结论不正确的是( )| A. | EF∥BC | B. | BC=2EF | C. | ∠AEF=∠B | D. | AE=AF |
13.给出正三角形、正方形、正五边形、正六边形四种形状的地砖,若只能选购其中的一种地砖来铺满地面,则可供选择的地砖共有( )
| A. | 4种 | B. | 3种 | C. | 2种 | D. | 1种 |
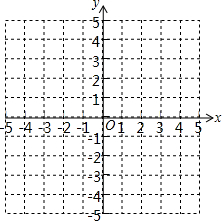 △ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将△ABC平移至△A1B1C1的位置,点A、B、C对应的点分别为A1、B1、C1,已知点A1的坐标是(-2,3).
△ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将△ABC平移至△A1B1C1的位置,点A、B、C对应的点分别为A1、B1、C1,已知点A1的坐标是(-2,3). 如图,EF∥AD,∠1=∠2,试说明AB∥DG.
如图,EF∥AD,∠1=∠2,试说明AB∥DG. 如图,将直角△ABC沿BC方向平移得到直角△DEF,其中AB=8,BE=10,DM=4,则阴影部分的面积是60.
如图,将直角△ABC沿BC方向平移得到直角△DEF,其中AB=8,BE=10,DM=4,则阴影部分的面积是60. 如图,水立方所在位置表示3街与3路的十字路口,玲珑塔所在位置表示4街与7路的十字路口.如果用(3,3)表示水立方的位置,那么“(3,3)→(3,4)→(3,5)→(3,6)→(3,7)→(4,7)”表示从水立方到玲珑塔的一种路线.请你用这种形式写出一种从水立方到玲珑塔的路线,且使该路线经过鸟巢:(3,3)→(4,3)→(5,3)→(5,4)→(5,5)→(5,6)→(5,7)→(4,7).
如图,水立方所在位置表示3街与3路的十字路口,玲珑塔所在位置表示4街与7路的十字路口.如果用(3,3)表示水立方的位置,那么“(3,3)→(3,4)→(3,5)→(3,6)→(3,7)→(4,7)”表示从水立方到玲珑塔的一种路线.请你用这种形式写出一种从水立方到玲珑塔的路线,且使该路线经过鸟巢:(3,3)→(4,3)→(5,3)→(5,4)→(5,5)→(5,6)→(5,7)→(4,7). 如图,等边△ABC的边长为1,在边AB上有一点P,Q为BC延长线上的一点,且CQ=PA,过点P作PE⊥AC于点E,连接PQ交AC于点D,则DE的长为$\frac{1}{2}$.
如图,等边△ABC的边长为1,在边AB上有一点P,Q为BC延长线上的一点,且CQ=PA,过点P作PE⊥AC于点E,连接PQ交AC于点D,则DE的长为$\frac{1}{2}$.