Question

9．在一次数学社团活动上，小明设计了一个社团标识，如图所示，正方形ABCD与折线D-E-F-B构成了中心对称图形，且DE⊥EF，AD=50，DE与EF长25，那么EF的长是10．

Answer 1

分析 连结BD，与EF交于点O，根据中心对称图形得到OE=$\frac{1}{2}$EF，OD=$\frac{1}{2}$BD，根据勾股定理得到BD，设EF=2x，则OE=x，DE=2x+25再在Rt△DOE中，根据勾股定理得到方程x²+（2x+25）²=（25$\sqrt{2}$）²，解方程即可求解．

解答 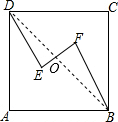解：连结BD，与EF交于点O，
∵正方形ABCD与折线D-E-F-B构成了中心对称图形，
∴OE=$\frac{1}{2}$EF，OD=$\frac{1}{2}$BD，
∵AD=50，
∴BD=$\sqrt{5{0}^{2}+5{0}^{2}}$=50$\sqrt{2}$，
∴OD=25$\sqrt{2}$，
设EF=2x，则OE=x，DE=2x+25，
在Rt△DOE中，x²+（2x+25）²=（25$\sqrt{2}$）²，
解得x=5或x=-25（舍去）．
则EF=5×2=10．
故答案为：10．

点评 此题考查了中心对称图形，勾股定理，解题的关键是作出辅助线，根据勾股定理得到方程x²+（2x+25）²=（25$\sqrt{2}$）²，注意方程思想的应用．