��Ŀ����
4��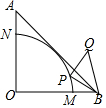 ��ͼ������Rt��AOB�У���AOB=90�㣬OA=$\sqrt{6}$����O��AB���У��ֱ�OA��OB��N��M����PBΪֱ�DZ�������Rt��BPQ����P�ڻ�MN���ɵ�M�˶�����N�����Q�˶���·����Ϊ��������
��ͼ������Rt��AOB�У���AOB=90�㣬OA=$\sqrt{6}$����O��AB���У��ֱ�OA��OB��N��M����PBΪֱ�DZ�������Rt��BPQ����P�ڻ�MN���ɵ�M�˶�����N�����Q�˶���·����Ϊ��������| A�� | $\frac{{\sqrt{3}}}{2}��$ | B�� | $\frac{{\sqrt{6}}}{3}��$ | C�� | $\sqrt{3}��$ | D�� | $\frac{{\sqrt{6}}}{2}��$ |
���� ����OP��AQ�����ݡ�ABO�͡�QBP��Ϊ����ֱ�������Σ����ɵó���ABQ�ס�OBP�������õ���BAQ=��BOP��$\frac{AQ}{OP}$=$\frac{AB}{OB}$�����AQ=$\sqrt{6}$�����ݵ�Q���˶��켣Ϊ��AΪԲ�ģ�AQ��Ϊ�뾶��Բ�Ľ�Ϊ90������εĻ��������ɵõ���Q�˶���·������
���  �⣺��ͼ������OP��AQ��
�⣺��ͼ������OP��AQ��
���O��AB������C������OC����OC��AB��
��OA=OB����AOB=90�㣬OB=$\sqrt{6}$��
��AB=2$\sqrt{3}$��OP=OC=$\frac{1}{2}$AB=$\sqrt{3}$��
�ߡ�ABO�͡�QBP��Ϊ����ֱ�������Σ�
��$\frac{BQ}{BP}$=$\frac{BA}{BO}$����ABO=��QBP=45�㣬
��$\frac{BQ}{BA}$=$\frac{BP}{BO}$����ABQ=��OBP��
���ABQ�ס�OBP��
���BAQ=��BOP��$\frac{AQ}{OP}$=$\frac{AB}{OB}$����$\frac{AQ}{\sqrt{3}}$=$\frac{2\sqrt{3}}{\sqrt{6}}$��
��AQ=$\sqrt{6}$��
�֡ߵ�P�ڻ�MN���ɵ�M�˶�����N��
��0��ܡ�BOP��90�㣬
��0��ܡ�BAQ��90�㣬
���Q���˶��켣Ϊ��AΪԲ�ģ�AQ��Ϊ�뾶��Բ�Ľ�Ϊ90������ε�Բ����
���Q�˶���·����Ϊ$\frac{90���С�\sqrt{6}}{180}$=$\frac{\sqrt{6}}{2}��$��
��ѡ��D��
���� ������Ҫ�����˹켣������ֱ�������ε������Լ����������ε��ж������ʵ����ã��������Ĺؼ����������߹������������Σ��������������εĶ�Ӧ�߳ɱ����Լ���Ӧ����ȣ��ó���Q���˶��켣��

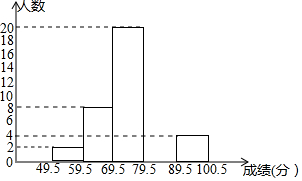 ijУ��ѧ��ȤС���Ա�����Ա�����ѧ����ĩ������ѧ�ɼ����ɼ�ȡ����������Ϊ100�֣�����ͳ�Ʒ�����ÿ���˵ijɼ�������ͬ�������Ƴ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���������ͼ���ṩ����Ϣ������������⣺
ijУ��ѧ��ȤС���Ա�����Ա�����ѧ����ĩ������ѧ�ɼ����ɼ�ȡ����������Ϊ100�֣�����ͳ�Ʒ�����ÿ���˵ijɼ�������ͬ�������Ƴ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���������ͼ���ṩ����Ϣ������������⣺��1��Ƶ����Ƶ�ʷֲ�����a=16��b=0.16 c=50��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3�����Ҫ���ð���ѧ����ĩ������ѧ�ɼ�������ͳ��ͼ����ô������69.5-79.5֮�������Բ�ĽǵĶ�����144��
��4������ͬѧ�ɼ�Ϊ79�֣���˵�������ǰ��ϱ��ҳɼ��ߵ��˻���$\frac{2}{5}$����Ҫ����Ŭ����������˵����ȷ����˵�����ɣ�
| ���� | 49.5��59.5 | 59.5��69.5 | 69.5��79.5 | 79.5��89.5 | 89.5��100.5 | �ϼ� |
| Ƶ�� | 2 | 8 | 20 | a | 4 | c |
| Ƶ�� | 0.04 | b | 0.40 | 0.32 | 0.08 | 1 |
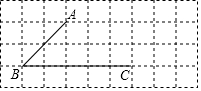 ��ͼ������С�����εı߳���Ϊ1��A��B��C���ڸ���ϣ�
��ͼ������С�����εı߳���Ϊ1��A��B��C���ڸ���ϣ�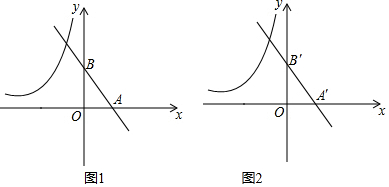
 ��ͼ����A��E��F��C��ͬһ��ֱ���ϣ�AB��CD��AE=FC����B=��D����֤��BF=DE��
��ͼ����A��E��F��C��ͬһ��ֱ���ϣ�AB��CD��AE=FC����B=��D����֤��BF=DE��