题目内容
6.关于x的方程x2-2mx+4=0有两个不同的实根,并且有一个根小于1,另一个根大于3,则实数m的取值范围为( )| A. | m>$\frac{5}{2}$ | B. | m<-$\frac{5}{2}$ | C. | m<-2 或 m>2 | D. | m>$\frac{13}{6}$ |
分析 首先设f(x)=x2-2mx+4,由关于x的方程x2-2mx+4=0有两个实数根,可得判别式△>0,则可求得m>2或m<-2,又由此二次函数的开口向上与两个实数根一个小于1,另一个大于3,可得f(1)<0,且f(3)<0,即可求得实数m的取值范围.
解答 解:∵x的方程x2-2mx+4=0有两个不同的实根,
∴△=4m2-16>0,
∴m>2或m<-2,
∵方程x2-2mx+4=0对应的二次函数,f(x)=x2-2mx+4的开口向上,而方程x2-2mx+4=0有两个不同的实根,并且有一个根小于1,另一个根大于3,
∴f(1)<0,且f(3)<0,
∴$\left\{\begin{array}{l}{1-2m+4<0}\\{9-6m+4<0}\end{array}\right.$,
∴m>$\frac{5}{2}$,
∵m>2或m<-2,
∴∴m>$\frac{5}{2}$,
故选A.
点评 此题考查了一元二次方根的分布,函数的性质与一元一次不等式(组)的解法.此题难度较大,解题的关键是掌握函数思想与数形结合思想的应用,还要注意二次函数的性质的灵活应用.

练习册系列答案
相关题目
19.下列是关于x的一元二次方程的是( )
| A. | $\frac{1}{{x}^{2}-5}=1$ | B. | (x-1)(x-5)=x2-5 | C. | x2=0 | D. | x2-2xy=1 |
14.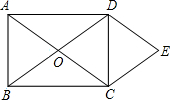 如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是( )
如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是( )
 如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是( )
如图,O为矩形ABCD对角线的交点,AD=8cm,AB=6cm,将△ABO向右平移得到△DCE,则△ABO向右平移过程中扫过的面积是( )| A. | 12cm2 | B. | 24cm2 | C. | 48cm2 | D. | 60cm2 |
11.已知2x=3y=4z,则x:y:z是( )
| A. | 2:3:4 | B. | 4:3:2 | C. | 7:6:5 | D. | 6:4:3 |
15.平面上直线a∥b,而直线b∥c,则直线a和c的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 以上都不对 |
 如图,正方形ABCD的边长为1,求阴影部分的面积?
如图,正方形ABCD的边长为1,求阴影部分的面积?