题目内容
17.双曲线y=-$\frac{1}{x}$上的两个点为(x1,y1),(x2,y2),且x1>x2>0,则y1与y2的大小关系是( )| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
分析 根据点的横坐标利用反比例函数图象上点的坐标特征即可用含x1、x2的代数式表示出y1、y2,结合x1>x2>0,即可得出y1与y2的大小关系.
解答 解:∵双曲线y=-$\frac{1}{x}$上的两个点为(x1,y1),(x2,y2),
∴y1=-$\frac{1}{{x}_{1}}$,y2=-$\frac{1}{{x}_{2}}$,
∵x1>x2>0,
∴-$\frac{1}{{x}_{1}}$>-$\frac{1}{{x}_{2}}$,
∴y1>y2.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征,根据反比例函数图象上点的坐标特征利用含x1、x2的代数式表示出y1、y2的值是解题的关键.

练习册系列答案
相关题目
7.已知抛物线y=ax2+bx+c的对称轴是x=2,且经过点(1,0),则9a+3b+c的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 3 |
12. 如图,在三角形ABC中,D为BC上一点,且BC=BD+AD,则D在线段( )的垂直平分线上.
如图,在三角形ABC中,D为BC上一点,且BC=BD+AD,则D在线段( )的垂直平分线上.
 如图,在三角形ABC中,D为BC上一点,且BC=BD+AD,则D在线段( )的垂直平分线上.
如图,在三角形ABC中,D为BC上一点,且BC=BD+AD,则D在线段( )的垂直平分线上.| A. | AB | B. | BC | C. | AC | D. | 以上都不对 |
2.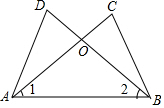 如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
 如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )| A. | AD=BC | B. | BD=AC | C. | ∠D=∠C | D. | OA=AB |
9. 如图,能使AB∥CD的条件是( )
如图,能使AB∥CD的条件是( )
 如图,能使AB∥CD的条件是( )
如图,能使AB∥CD的条件是( )| A. | ∠1=∠B | B. | ∠3=∠A | C. | ∠BCD+∠B=180° | D. | ∠1=∠A |
7.用四舍五入法按要求对2.04607分别取近似值,其中错误的是( )
| A. | 2(精确到个位) | B. | 2.05(精确到百分位) | ||
| C. | 2.1(精确到0.1) | D. | 2.0461(精确到0.0001) |