题目内容
在抛物线y=x(a-x )与x轴所围图形的内接矩形(一边在x轴上)中(其中a为常数),周长最大的两边之长分别为 .
考点:抛物线与x轴的交点
专题:计算题,探究型,函数思想
分析:如图,设B(x,0),0<x<
,然后根据已知条件可以分别用x表示相等BC、AB的长度,接着就可以用x表示矩形ABCD的周长,最后利用二次函数的性质即可解决问题.
| a |
| 2 |
解答:解:题中的矩形ABCD如图所示,
设B(x,0),0<x<
,
则C(a-x,0),
则BC=(a-x)-x=a-2x,AB=x(a-x),
∴矩形周长C=2[x(a-x)+(a-2x)]
=-2(x-
)2+
,
当x=
时,即BC=2,AB=
时,周长最大.
故答案为:2,
.

设B(x,0),0<x<
| a |
| 2 |
则C(a-x,0),
则BC=(a-x)-x=a-2x,AB=x(a-x),
∴矩形周长C=2[x(a-x)+(a-2x)]
=-2(x-
| a-2 |
| 2 |
| a2+4 |
| 2 |
当x=
| a-2 |
| 2 |
| a2-4 |
| 4 |
故答案为:2,
| a2-4 |
| 4 |
点评:此题主要考查了抛物线与x轴的交点坐标,解题的关键是利用交点坐标分别表示线段的长度,最后利用二次函数的最值即可求解.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
方程|x2-1|=
(x+
)的实根个数为( )
| 1 |
| 10 |
| 9 |
| 10 |
| A、4 | B、3 | C、2 | D、1 |
小李年初向建设银行贷款5万元用于购房,年利率为5%,按复利计算,若这笔借款分15次等额归还,每年1次,15年还清,并从借后次年年初开始归还,问每年应还大约( )
| A、4819元 |
| B、4818元 |
| C、4817元 |
| D、4816元 |
某三角形的三条边长为三个连续自然数,若它的周长不超过13,则符合要求的三角形共有( )
| A、1组 | B、2组 | C、3组 | D、4组 |
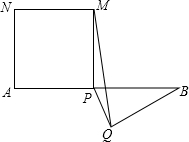 如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于
如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于