题目内容
7.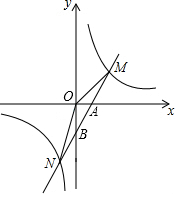 如图所示,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(-2,-8),一次函数y=ax+b与x轴交于点A,与y轴交于点B.
如图所示,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(-2,-8),一次函数y=ax+b与x轴交于点A,与y轴交于点B.(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
分析 (1)由点N的坐标求出k的值,即可得出反比例函数的解析式;由反比例函数解析式求出m=4,由待定系数法求出一次函数解析式即可;
(2)由一次函数解析式求出点A(2,0),△MON的面积=△AOM的面积+△AOM的面积,即可得出结果;
(3)由图象容易得出结论.
解答 解:(1)由题意得:-8=$\frac{k}{-2}$,
∴k=16,
∴反比例函数的解析式是y=$\frac{16}{x}$;
∵反比例函数过M(4,m),
∴m=$\frac{16}{4}$=4,
∵一次函数y=ax+b的图象过点M(4,m)和N(-2,-8),
∴$\left\{\begin{array}{l}{4a+b=4}\\{-2a+b=-8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=-4}\end{array}\right.$,
∴一次函数解析式是y=2x-4;
(2)∵点A在一次函数图象上,
∴当y=0时,x=2,
∴A(2,0),
∴△MON的面积=△AOM的面积+△AOM的面积=$\frac{1}{2}$×2×8+$\frac{1}{2}$×2×4=12;
(3)由图象可知,当x<-2或0<x<4时,反比例函数的值大于一次函数的值.
点评 本题主要考查对用待定系数法求一次函数、反比例函数的解析式,解一元一次方程,解二元一次方程组,一次函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

练习册系列答案
相关题目
19. 元旦将至,某果品批发公司为指导今年的芒果销售,对往年市场销售情况进行了调查统计,得到如下数据:
元旦将至,某果品批发公司为指导今年的芒果销售,对往年市场销售情况进行了调查统计,得到如下数据:
(1)在如图所示的直角坐标系中,描出各组有序数对(x,y)所对应的点.连接各点,判断这些点是否能在一条直线上,如果能,求出y与x之间的函数关系式,如果不能,请说明理由.
(2)该公司今年要获得3.15万元的利润,且保证芒果销售量不少于4000千克,已知芒果进价为13元/千克,求出今年芒果的销售价x的值.
 元旦将至,某果品批发公司为指导今年的芒果销售,对往年市场销售情况进行了调查统计,得到如下数据:
元旦将至,某果品批发公司为指导今年的芒果销售,对往年市场销售情况进行了调查统计,得到如下数据:| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
(2)该公司今年要获得3.15万元的利润,且保证芒果销售量不少于4000千克,已知芒果进价为13元/千克,求出今年芒果的销售价x的值.
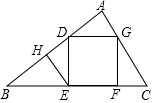 已知:如图,正方形DEFG内接于Rt△ABC,EF在斜边BC上,EH⊥AB于H.
已知:如图,正方形DEFG内接于Rt△ABC,EF在斜边BC上,EH⊥AB于H. 已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5).
已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5).