题目内容
20.当m为何值时,关于x的方程$\frac{2}{x-2}+\frac{mx}{{{x^2}-4}}=\frac{3}{x+2}$无解?分析 方程两边都乘以(x+2)(x-2)把分式方程化为整式方程,得出x=$\frac{10}{1-m}$,再根据x=2或x=-2时方程无解,得出$\frac{10}{1-m}$=2或$\frac{10}{1-m}$=-2,求出m的值即可.
解答 解:方程两边都乘以(x+2)(x-2)去分母得,
2(x+2)+mx=3(x-2),
整理得,(1-m)x=10,
解得:x=$\frac{10}{1-m}$,
∵1-m=0时,$\frac{10}{1-m}$无意义,
∴当m=1时,原方程无解,
∵x=2或-2时方程无解,
∴$\frac{10}{1-m}$=2或$\frac{10}{1-m}$=-2,
解得:m=-4或m=6,
∴当m=1、m=-4或m=6时,关于x的方程$\frac{2}{x-2}+\frac{mx}{{{x^2}-4}}=\frac{3}{x+2}$无解.
点评 本题考查了分式方程的解,要注意分式方程的解不能使最简公分母等于0.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
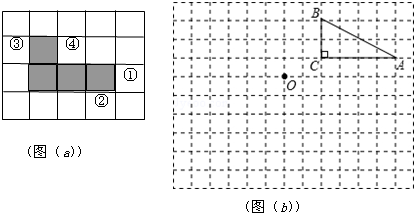
 如图,已知AO⊥BC,DO⊥OE,若∠1=56°,则∠2=56°.
如图,已知AO⊥BC,DO⊥OE,若∠1=56°,则∠2=56°.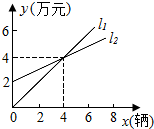 如图,l1表示某品牌电动车厂一天的销售收入与电动车销售量的关系;l2表示该电动车厂一天的销售成本与销售量的关系.
如图,l1表示某品牌电动车厂一天的销售收入与电动车销售量的关系;l2表示该电动车厂一天的销售成本与销售量的关系.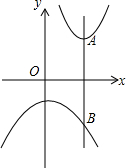 如图,在平面直角坐标系中,抛物线y=a(x-3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=-$\frac{1}{3}$x2-2于点B,则A、B两点间的距离为7.
如图,在平面直角坐标系中,抛物线y=a(x-3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=-$\frac{1}{3}$x2-2于点B,则A、B两点间的距离为7.