题目内容
10.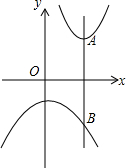 如图,在平面直角坐标系中,抛物线y=a(x-3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=-$\frac{1}{3}$x2-2于点B,则A、B两点间的距离为7.
如图,在平面直角坐标系中,抛物线y=a(x-3)2+2(a>0)的顶点为A,过点A作y轴的平行线交抛物线y=-$\frac{1}{3}$x2-2于点B,则A、B两点间的距离为7.
分析 先求得顶点A的坐标,然后根据题意得出B的横坐标,把横坐标代入抛物线y=-$\frac{1}{3}$x2-2,得出纵坐标,从而求得A、B间的距离.
解答 解:∵抛物线y=a(x-3)2+2(a>0)的顶点为A,
∴A(3,2),
∵过点A作y轴的平行线交抛物线y=-$\frac{1}{3}$x2-2于点B,
∴B的横坐标为3,
把x=3代入y=-$\frac{1}{3}$x2-2得y=-5,
∴B(3,-5),
∴AB=2+5=7.
故答案为7.
点评 本题考查了二次函数图象上点的坐标特征,求得A、B的坐标是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
1.下列各组数中,互为相反数的是( )
| A. | (-2)-3与23 | B. | (-2)-2与2-2 | C. | -33与(-$\frac{1}{3}$)3 | D. | (-3)-3与($\frac{1}{3}$)3 |
5.下列命题中,属于假命题的是( )
| A. | 两点确定一条直线 | B. | 负数的偶次幂是正数 | ||
| C. | 锐角的补角是钝角 | D. | 若|-x|=-x,则x的值为0 |
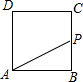 如图,已知正方形ABCD的边长为4,现有一动点P从点B出发,沿着B→C→D→A的路径以每秒1个单位长度的速度运动,则S△PAB与运动时间t(秒)之间的函数关系图象是( )
如图,已知正方形ABCD的边长为4,现有一动点P从点B出发,沿着B→C→D→A的路径以每秒1个单位长度的速度运动,则S△PAB与运动时间t(秒)之间的函数关系图象是( )
 在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边长为x米,镶有花边后,整个地毯EFGH中FG边长为y米.
在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边长为x米,镶有花边后,整个地毯EFGH中FG边长为y米.