题目内容
15.计算或化简:①计算($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$.
②已知a≠0,且满足a2-3a+1=0,求a2+$\frac{1}{{a}^{2}}$的值.
分析 ①原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
②已知等式整理求出a+$\frac{1}{a}$的值,再利用完全平方公式即可求出所求式子的值.
解答 解:①原式=-$\frac{a-(a-b)}{(a+b)(a-b)}$•$\frac{a-b}{b}$
=-$\frac{1}{a+b}$;
②已知等式整理得:a+$\frac{1}{a}$=3,
两边平方得:(a+$\frac{1}{a}$)2=a2+$\frac{1}{{a}^{2}}$+2=9,
则a2+$\frac{1}{{a}^{2}}$=7.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
5.下列命题中,属于假命题的是( )
| A. | 两点确定一条直线 | B. | 负数的偶次幂是正数 | ||
| C. | 锐角的补角是钝角 | D. | 若|-x|=-x,则x的值为0 |
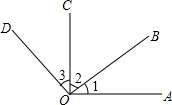 如图,已知OA⊥OC,OB⊥OD,∠3=24°,求:∠1、∠2的度数.
如图,已知OA⊥OC,OB⊥OD,∠3=24°,求:∠1、∠2的度数. 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算: