题目内容
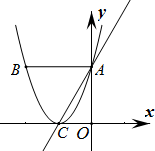 如图所示,抛物线y1=
如图所示,抛物线y1=| 3 |
(1)求直线AC的解析式y2=kx+b;
(2)求△ABC的面积;
(3)当自变量x满足什么条件时,有y1>y2.
考点:二次函数与不等式(组),待定系数法求一次函数解析式,二次函数的性质
专题:
分析:(1)先求出点A、C的坐标,再利用待定系数法求一次函数解析式解答;
(2)根据二次函数的对称性和点A的坐标求出点B的坐标,然后求出AB,再利用三角形的面积公式列式计算即可得解;
(3)写出抛物线在直线上方部分的x的取值范围即可.
(2)根据二次函数的对称性和点A的坐标求出点B的坐标,然后求出AB,再利用三角形的面积公式列式计算即可得解;
(3)写出抛物线在直线上方部分的x的取值范围即可.
解答:解:(1)∵抛物线y=
(x+1)2的顶点为C,
∴点C的坐标为(-1,0),
令x=0,则y=
,
所以,点A的坐标为(0,
),
将点A、C的坐标代入直线解析式得,
,
解得
,
所以,直线AC的解析式为y=
x+
;
(2)∵顶点坐标为(-1,0),
∴对称轴为直线x=-1,
∵AB⊥y轴,
∴点A、B关于对称轴对称,
∴点B的坐标为(-2,
),
∴AB=2,
∴△ABC的面积=
×2×
=
;
(3)由图可知,x<-1或x>0时,y1>y2.
| 3 |
∴点C的坐标为(-1,0),
令x=0,则y=
| 3 |
所以,点A的坐标为(0,
| 3 |
将点A、C的坐标代入直线解析式得,
|
解得
|
所以,直线AC的解析式为y=
| 3 |
| 3 |
(2)∵顶点坐标为(-1,0),
∴对称轴为直线x=-1,
∵AB⊥y轴,
∴点A、B关于对称轴对称,
∴点B的坐标为(-2,
| 3 |
∴AB=2,
∴△ABC的面积=
| 1 |
| 2 |
| 3 |
| 3 |
(3)由图可知,x<-1或x>0时,y1>y2.
点评:本题考查了二次函数与不等式,待定系数法求一次函数解析式,二次函数的对称性,熟练掌握各性质与待定系数法求函数解析式是解题的关键,难点在于(2)求出点B的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各数中互为相反数的是( )
| A、-2与+(-2) |
| B、-(-1)与+(+1) |
| C、(-2)2与-22 |
| D、(-2)3与-23 |
某校2013年给希望工程捐款2万元,以后每年都捐款,计划到2015年三年总共捐款6.62万元,若设该校捐款的年平均增长率为x,则可列方程为( )
| A、2+2x2(1+x)=6.62 |
| B、2(1+x)2=6.62 |
| C、2+2(1+x)+2(1+x)2=6.62 |
| D、2(1+x)3=6.62 |
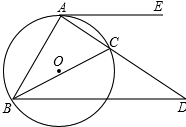 △ABC内接于⊙O,AE切⊙O于A,过B作BD平行AE交AC延长线于D,若AC=4cm CD=3cm,求AB的长.
△ABC内接于⊙O,AE切⊙O于A,过B作BD平行AE交AC延长线于D,若AC=4cm CD=3cm,求AB的长.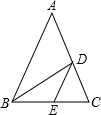 如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是
如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是 如图,圆内接正五边形ABCDE的半径为2,连接AC、BD相交于点F.
如图,圆内接正五边形ABCDE的半径为2,连接AC、BD相交于点F.
 如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与x轴的交点.
如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与x轴的交点.