题目内容
 如图,圆内接正五边形ABCDE的半径为2,连接AC、BD相交于点F.
如图,圆内接正五边形ABCDE的半径为2,连接AC、BD相交于点F.(1)求证:AB=AF;
(2)求
 |
| AB |
考点:正多边形和圆
专题:
分析:(1)根据正五边形的性质求出∠ABD、∠ACB、∠DBC的度数,借助三角形的外角性质即可解决问题.
(2)根据
的长为圆周长的
,求出圆的周长,即可解决问题.
(2)根据
 |
| AB |
| 1 |
| 5 |
解答: 解:(1)∵五边形ABCDE为正五边形,
解:(1)∵五边形ABCDE为正五边形,
∴
=
=
=
=
=
⊙O的周长,
∴∠ABD=
×
×360°=72°,
∠ACB=∠DBC=
×
×360°=36°,
∴∠AFB=2×36°=72°,
∴∠ABF=∠AFB,
∴AB=AF.
(2)∵⊙O的周长=2π×2=4π,
∴
的长=
×4π=
.
 解:(1)∵五边形ABCDE为正五边形,
解:(1)∵五边形ABCDE为正五边形,∴
 |
| AB |
 |
| BC |
 |
| CD |
 |
| DE |
 |
| AE |
| 1 |
| 5 |
∴∠ABD=
| 1 |
| 2 |
| 2 |
| 5 |
∠ACB=∠DBC=
| 1 |
| 2 |
| 1 |
| 5 |
∴∠AFB=2×36°=72°,
∴∠ABF=∠AFB,
∴AB=AF.
(2)∵⊙O的周长=2π×2=4π,
∴
 |
| AB |
| 1 |
| 5 |
| 4π |
| 5 |
点评:该命题考查了圆内接正多边形的性质及其应用问题;解题的关键是灵活运用圆周角定理等几何知识点来分析、判断、解答.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
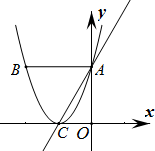 如图所示,抛物线y1=
如图所示,抛物线y1= 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x<3时,y>0.正确的是
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x<3时,y>0.正确的是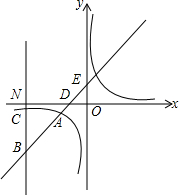 如图,一次函数y=kx+1(k≠0)与反比例函数y=
如图,一次函数y=kx+1(k≠0)与反比例函数y= 如图:BO为Rt△ABC斜边AC上的中线,G为Rt△ABC的重心,连结AG并延长交BC于D,若AB=6cm,BC=8cm,则OG的长为
如图:BO为Rt△ABC斜边AC上的中线,G为Rt△ABC的重心,连结AG并延长交BC于D,若AB=6cm,BC=8cm,则OG的长为