题目内容
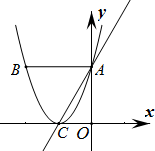
 如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与x轴的交点.
如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与x轴的交点.(1)求点B的坐标.
(2)求△AOB的面积.
考点:一次函数图象上点的坐标特征
专题:
分析:(1)利用待定系数法把A点坐标代入y=kx+5中即可算出k的值,然后联立两个函数解析式,即可算出B点坐标;
(2)根据A、B两点的坐标和三角形的面积公式进行计算即可.
(2)根据A、B两点的坐标和三角形的面积公式进行计算即可.
解答:解:(1)把A(1,4)代入y=kx+5中得:4=k+5,
解得:k=-1,
则一次函数解析式为y=-x+5,
令y=0,则0=-x+5,
解得x=5,
故B点坐标是(5,0);
(2)∵A(1,4),B(5,0);
∴S△AOB=
×OB×yA=
×5×4=10.
解得:k=-1,
则一次函数解析式为y=-x+5,
令y=0,则0=-x+5,
解得x=5,
故B点坐标是(5,0);
(2)∵A(1,4),B(5,0);
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了一次函数的坐标特征以及与坐标轴交点问题,涉及的知识有:坐标与图形性质,直线与坐标轴的交点,待定系数法求函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
对于函数y=4x2,下列说法正确的是( )
| A、当x>0时,y随x的增大而减小 |
| B、当x<0时,y随x的增大而减小 |
| C、y随x的增大而减小 |
| D、y随x的增大而增大 |
 如图所示,抛物线y1=
如图所示,抛物线y1= 如图,一次函数y=kx+1(k≠0)与反比例函数y=
如图,一次函数y=kx+1(k≠0)与反比例函数y= 如图,点C在线段AB上,BC=2AC,M、N是AC、BC中点,若AB=a,求BC-MN.
如图,点C在线段AB上,BC=2AC,M、N是AC、BC中点,若AB=a,求BC-MN. 如图:BO为Rt△ABC斜边AC上的中线,G为Rt△ABC的重心,连结AG并延长交BC于D,若AB=6cm,BC=8cm,则OG的长为
如图:BO为Rt△ABC斜边AC上的中线,G为Rt△ABC的重心,连结AG并延长交BC于D,若AB=6cm,BC=8cm,则OG的长为 如图为直径20cm的圆柱形油槽,装入油后,油深CD为8cm,那么油面宽度AB=
如图为直径20cm的圆柱形油槽,装入油后,油深CD为8cm,那么油面宽度AB=