题目内容
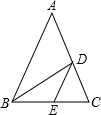 如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是
如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上,BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE的周长是考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:由平行和角平分线可得∠EDB=∠EBD,可得DE=BE,又由AB=AC,DE∥AB可得∠DEC=∠C,可得DE=DC,则可求出△CDE的周长.
解答:解:∵DE∥AB,BD平分∠ABC,
∴∠EBD=∠ABD=∠EDB,
∴DE=BE=5cm,
∵AB=AC,DE∥AB,
∴∠C=∠ABE=∠DEC,
∴DC=DE=5cm,且CE=3cm,
∴DE+EC+CD=5cm+3cm+5cm=13cm,
即△CDE的周长为13cm,
故答案为:13cm.
∴∠EBD=∠ABD=∠EDB,
∴DE=BE=5cm,
∵AB=AC,DE∥AB,
∴∠C=∠ABE=∠DEC,
∴DC=DE=5cm,且CE=3cm,
∴DE+EC+CD=5cm+3cm+5cm=13cm,
即△CDE的周长为13cm,
故答案为:13cm.
点评:本题主要考查等腰三角形的判定和性质,由条件得到DE=DC=BE是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
对于函数y=4x2,下列说法正确的是( )
| A、当x>0时,y随x的增大而减小 |
| B、当x<0时,y随x的增大而减小 |
| C、y随x的增大而减小 |
| D、y随x的增大而增大 |
 如图,一次函数y=-
如图,一次函数y=- 如图,Rt△ABC的内切圆⊙O与斜边AB切于点D,与两直角分别切于点E、S,DE与AC的延长线交于点F,请判断BD与CF有何关系?写出你的猜想,并加以证明.
如图,Rt△ABC的内切圆⊙O与斜边AB切于点D,与两直角分别切于点E、S,DE与AC的延长线交于点F,请判断BD与CF有何关系?写出你的猜想,并加以证明. 如图所示,抛物线y1=
如图所示,抛物线y1=