题目内容
某校2013年给希望工程捐款2万元,以后每年都捐款,计划到2015年三年总共捐款6.62万元,若设该校捐款的年平均增长率为x,则可列方程为( )
| A、2+2x2(1+x)=6.62 |
| B、2(1+x)2=6.62 |
| C、2+2(1+x)+2(1+x)2=6.62 |
| D、2(1+x)3=6.62 |
考点:由实际问题抽象出一元二次方程
专题:增长率问题
分析:2014年的捐款是2(1+x)万元,2015年的捐款数是2(1+x)2,本题首先由题意得出题中的等量关系即三年共捐款6.62万元,列出方程即可.
解答:解:设该校捐款的平均年增长率为x.
则:2+2(1+x)+2(1+x)2=6.62,
故选:C.
则:2+2(1+x)+2(1+x)2=6.62,
故选:C.
点评:本题考查数量平均变化率问题,解题的关键是正确列出一元二次方程.原来的数量为a,平均每次增长或降低的百分率为x的话,经过第一次调整,就调整到a×(1±x),再经过第二次调整就是a×(1±x)(1±x)=a(1±x)2.增长用“+”,下降用“-”.

练习册系列答案
相关题目
下列各式计算正确的是( )
| A、-(-42)=-16 | ||||||||
| B、-8-2×6=(-1+6)×(-2) | ||||||||
C、4÷
| ||||||||
| D、(-1)2003+(-1)2004=-1+1 |
如果单项式
x3ya与xby4是同类项,那么(-a)b的值是( )
| 2 |
| 3 |
| A、64 | B、-64 |
| C、81 | D、-81 |
 如图,点M,N在边长为9的正方形纸片ABCD的边上,将正方形沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,若B′C=3,求AM的长.(提示:连接BM,MB′)
如图,点M,N在边长为9的正方形纸片ABCD的边上,将正方形沿MN折叠,使点B落在CD边上的B′处,点A对应点为A′,若B′C=3,求AM的长.(提示:连接BM,MB′) 如图,直径AB⊥弦CD于E,AE=2cm,CE=4cm.求⊙O半径的长.
如图,直径AB⊥弦CD于E,AE=2cm,CE=4cm.求⊙O半径的长.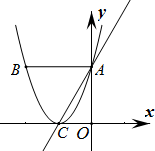 如图所示,抛物线y1=
如图所示,抛物线y1= 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x<3时,y>0.正确的是
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x<3时,y>0.正确的是