题目内容
1.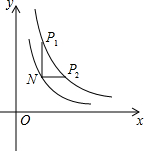 如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )| A. | $\frac{1}{2}$或2 | B. | $\frac{1}{2}$或8 | C. | 2或6 | D. | 2或8 |
分析 由P1N∥y轴,P2N∥x轴得到P1的横坐标为m,P2的纵坐标为n,再根据反比例函数图象上点的坐标特征得P1(m,$\frac{4}{m}$),P2($\frac{4}{n}$,n),则NP1=$\frac{4}{m}$-n,NP2=$\frac{4}{n}$-m,所以($\frac{4}{m}$-n)($\frac{4}{n}$-m)=2,解关于mn的一元二次方程得mn=2或mn=8,加上点N(m,n)在反比例函数y=$\frac{k}{x}$的图象上,则k=mn,于是可得k=2或8.
解答 解:∵P1N∥y轴,P2N∥x轴,
∴P1的横坐标为m,P2的纵坐标为n,
而点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,
∴P1(m,$\frac{4}{m}$),P2($\frac{4}{n}$,n),
∴NP1=$\frac{4}{m}$-n,NP2=$\frac{4}{n}$-m,
∴($\frac{4}{m}$-n)($\frac{4}{n}$-m)=2,
整理得(mn)2-10mn+16=0,解得mn=2或mn=8,
∵点N(m,n)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=mn,
∴k=2或8.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.计算$\frac{1}{x-1}$+$\frac{x}{1-x}$的结果是( )
| A. | x-1 | B. | 1-x | C. | 1 | D. | -1 |
11. 如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,则∠BOC与∠A的大小关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,则∠BOC与∠A的大小关系是( )
 如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,则∠BOC与∠A的大小关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,则∠BOC与∠A的大小关系是( )| A. | ∠BOC=2∠A | B. | ∠BOC=90°+∠A | C. | ∠BOC=90°+$\frac{1}{2}$∠A | D. | ∠BOC=90°-$\frac{1}{2}$∠A |
 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?
小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问:从小华家到学校的平路和下坡路各有多远?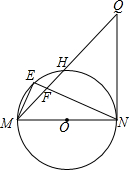 如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为$\widehat{MH}$上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN.
如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为$\widehat{MH}$上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN. 如图,点A在双曲线y=$\frac{k}{x}$上,AB⊥x轴于点B,且△AOB的面积是2,则k的值是-4.
如图,点A在双曲线y=$\frac{k}{x}$上,AB⊥x轴于点B,且△AOB的面积是2,则k的值是-4.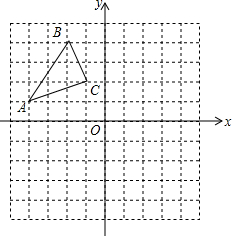 在如图所示的平面直角坐标系中,每个小正方形的边长均为1,△ABC的顶点都在格点上.
在如图所示的平面直角坐标系中,每个小正方形的边长均为1,△ABC的顶点都在格点上.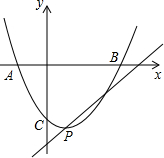 已知抛物线y=ax2-2ax+c与x轴交于A、B两点,与y轴交于点C.其中.A(-1,0),C(0,-3).
已知抛物线y=ax2-2ax+c与x轴交于A、B两点,与y轴交于点C.其中.A(-1,0),C(0,-3).