题目内容
6.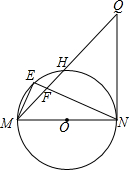 如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为$\widehat{MH}$上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN.
如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为$\widehat{MH}$上一点,连接ME,NE,NE交MQ于点F,且ME2=EF•EN.(1)求证:QN=QF;
(2)若点E到弦MH的距离为1,cos∠Q=$\frac{3}{5}$,求⊙O的半径.
分析 (1)如图1,通过相似三角形(△MEF∽△MEN)的对应角相等推知,∠1=∠EMN;又由弦切角定理、对顶角相等证得∠2=∠3;最后根据等角对等边证得结论;
(2)如图2,连接OE交MQ于点G,设⊙O的半径是r.根据(1)中的相似三角形的性质证得∠EMF=∠ENM,所以由“圆周角、弧、弦间的关系”推知点E是弧MH的中点,则OE⊥MQ;然后通过解直角△MNE求得cos∠Q=sin∠GMO=$\frac{r-1}{r}$=$\frac{3}{5}$,则可以求r的值.
解答 (1)证明:如图1,
∵ME2=EF•EN,
∴$\frac{ME}{EN}$=$\frac{EF}{ME}$.
又∵∠MEF=∠MEN,
∴△MEF∽△MEN,
∴∠1=∠EMN.
∵∠1=∠2,∠3=∠EMN,
∴∠2=∠3,
∴QN=QF;
(2)解:如图2,连接OE交MQ于点G,设⊙O的半径是r.
由(1)知,△MEF∽△MEN,则∠4=∠5.
∴$\widehat{ME}$=$\widehat{EH}$.
∴OE⊥MQ,
∴EG=1.
∵cos∠Q=$\frac{3}{5}$,且∠Q+∠GMO=90°,
∴sin∠GMO=$\frac{3}{5}$,
∴$\frac{OG}{OM}$=$\frac{3}{5}$,即$\frac{r-1}{r}$=$\frac{3}{5}$,
解得,r=2.5,即⊙O的半径是2.5.
点评 本题考查切线的性质和相似三角形的判定与性质.在(1)中判定△MEF∽△MEN是解题的关键,在(2)中推知点E是弧MH的中点是解题的关键.

练习册系列答案
相关题目
16.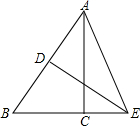 如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
 如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )
如图,Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为( )| A. | $\frac{7}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{3}$ |
17. 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切 | D. | 以上三种情况均有可能 |
14.已知反比例函数y=$\frac{k}{x}$的图象经过点(3,2),那么下列四个点中,也在这个函数图象上的是( )
| A. | (3,-2) | B. | (-2,-3) | C. | (1,-6) | D. | (-6,1) |
1.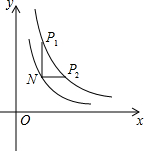 如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
 如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )| A. | $\frac{1}{2}$或2 | B. | $\frac{1}{2}$或8 | C. | 2或6 | D. | 2或8 |