题目内容
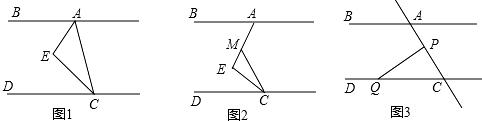
11. 如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,则∠BOC与∠A的大小关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,则∠BOC与∠A的大小关系是( )| A. | ∠BOC=2∠A | B. | ∠BOC=90°+∠A | C. | ∠BOC=90°+$\frac{1}{2}$∠A | D. | ∠BOC=90°-$\frac{1}{2}$∠A |
分析 首先根据BO,CO分别平分∠ABC和∠ACB,推得∠0BC+∠0CB=$\frac{1}{2}$(∠ABC+∠ACB)=90°-$\frac{1}{2}$∠A;然后根据三角形的内角和定理,判断∠BOC与∠A的大小关系即可.
解答 解:∵BO平分∠ABC,CO平分∠ACB,
∴∠OBC=$\frac{1}{2}∠ABC$,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB))=$\frac{1}{2}$(180°-∠A)=90°$-\frac{1}{2}$∠A,
根据三角形的内角和定理,可得
∠OBC+∠OCB+∠BOC=180°,
∴90°-$\frac{1}{2}$∠A+∠BOC=180°,
∴∠BOC=90°+$\frac{1}{2}$∠A.
故选:C.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:一个角的平分线把这个角分成两个大小相同的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.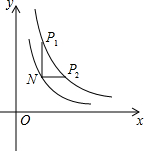 如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
 如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )
如图,点P1,P2是反比例函数图象y=$\frac{4}{x}$上任意两点,过点P1作y轴的平行线,与过点P2作x轴的平行线相交于点N,若点N(m,n)恰好在另一个反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,且NP1•NP2=2,则k的值为( )| A. | $\frac{1}{2}$或2 | B. | $\frac{1}{2}$或8 | C. | 2或6 | D. | 2或8 |
19.下列调查:
①企业招聘,对招聘人员进行面试;
②调查全班同学的身高;
③调查市场上某种食品的色素含量是否符合国家标准;
④调查一批灯泡的使用寿命;
其中符合用全面调查的是( )
①企业招聘,对招聘人员进行面试;
②调查全班同学的身高;
③调查市场上某种食品的色素含量是否符合国家标准;
④调查一批灯泡的使用寿命;
其中符合用全面调查的是( )
| A. | ①② | B. | ①③ | C. | ②④ | D. | ②③ |
6.下列计算正确的是( )
| A. | $\sqrt{\frac{5}{3}}$=$\frac{1}{3}$$\sqrt{5}$ | B. | $\sqrt{54}$•$\sqrt{\frac{1}{2}}$=$\frac{3}{2}\sqrt{6}$ | C. | $\frac{\sqrt{24}}{\sqrt{3}}$=$\sqrt{2}$ | D. | 3$\sqrt{2a}$-$\sqrt{8a}$=$\sqrt{2a}$ |
16.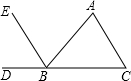 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )| A. | ∠C=75° | B. | ∠DBE=75° | C. | ∠ABE=75° | D. | ∠EBC=105° |