题目内容
5. 如图,将△ABC绕点B顺时针旋转到△EBD的位置,且BA∥DE,DE的延长线交BC于点F,若BD=8,DE=6,则EF=$\frac{14}{3}$.
如图,将△ABC绕点B顺时针旋转到△EBD的位置,且BA∥DE,DE的延长线交BC于点F,若BD=8,DE=6,则EF=$\frac{14}{3}$.
分析 根据旋转的性质得到∠DBE=∠ABC,根据平行线的性质得到∠ABC=∠BFD,等量代换得到∠DBE=∠BFD,根据相似三角形的性质得到DF=$\frac{32}{3}$,于是得到结论.
解答 解:∵将△ABC绕点B顺时针旋转到△EBD的位置,
∴∠DBE=∠ABC,
∵AB∥DE,
∴∠ABC=∠BFD,
∴∠DBE=∠BFD,
∵∠D=∠D,
∴△BDE∽△FDB,
∴$\frac{BD}{DF}=\frac{DE}{BD}$,即$\frac{8}{DF}$=$\frac{6}{8}$,
∴DF=$\frac{32}{3}$,
∴EF=DF-DE=$\frac{14}{3}$.
故答案为:$\frac{14}{3}$.
点评 本题考查了旋转的性质,相似三角形的判定和性质,平行线的性质,熟练掌握旋转的性质是解题的关键.

练习册系列答案
相关题目
17.若关于x的不等式组$\left\{\begin{array}{l}{x≥a}\\{\frac{x-1}{2}-\frac{2x-1}{6}<1}\end{array}\right.$的解集中只含有3个整数解,则a的取值范围是( )
| A. | -2<a≤-1 | B. | -2≤a<-1 | C. | 5<a≤6 | D. | 5≤a<6 |
 如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点C逆时针旋转α(0°<α<90°),得到△MNC,连接BM,当BM⊥AC,则旋转角α的度数为60°.
如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点C逆时针旋转α(0°<α<90°),得到△MNC,连接BM,当BM⊥AC,则旋转角α的度数为60°. 如图,△ABC与△A1B1C1是位似图形.
如图,△ABC与△A1B1C1是位似图形. 如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,BD⊥OA,且OA•BD=$\frac{9}{2}$,则k的值为$\frac{3}{2}$.
如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,BD⊥OA,且OA•BD=$\frac{9}{2}$,则k的值为$\frac{3}{2}$.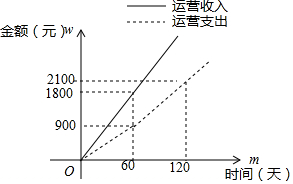 环保健康的“共享单车”已成为人们短途出行的一种新方式,一辆新投放市场的单车其先期成本为1050元.如图是一辆新投放的共享单车其运营收入w1和运营支出w2关于时间m的函数图象.
环保健康的“共享单车”已成为人们短途出行的一种新方式,一辆新投放市场的单车其先期成本为1050元.如图是一辆新投放的共享单车其运营收入w1和运营支出w2关于时间m的函数图象. 如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1.
如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1.