题目内容
17.已知抛物线y=(a2+1)x2+bx+c与x轴相交于A、B两点.且AB=6,抛物线的对称轴为直线x=-1.则当函数值y>0时.对应的自变量x的取值范围是x<-4或x>2.分析 根据抛物线的对称性得到A(-4,0),B(2,0),由a2+1>0,得到抛物线y=(a2+1)x2+bx+c的开口向上,得到当函数值y>0时,图象在x 轴的上方,于是得到结论.
解答 解:∵AB=6,抛物线的对称轴为直线x=-1,
∴A(-4,0),B(2,0),
∵a2+1>0,
∴抛物线y=(a2+1)x2+bx+c的开口向上,
∴当函数值y>0时,图象在x 轴的上方,
∴自变量x的取值范围是:x<-4或x>2,
故答案为:x<-4或x>2.
点评 本题考查了二次函数的图象与x轴的交点问题、以及抛物线的对称问题.解决本题的关键是正确的理解并应用抛物线与x轴的交点横坐标.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.在如图中,表示数轴正确的是( )
| A. |  | B. |  | C. |  | D. |  |
7.甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
且${\overline x_乙}$=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是7,中位数是7.5.
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
| 甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
| 乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
(1)乙运动员射击训练成绩的众数是7,中位数是7.5.
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
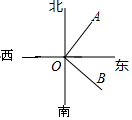 如图,在点O北偏东65°的某处有一点A,在点O南东20°的某处有一点B,则∠AOB的度数是95°.
如图,在点O北偏东65°的某处有一点A,在点O南东20°的某处有一点B,则∠AOB的度数是95°. 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3$\sqrt{3}$.其中正确的结论是①②③.
如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3$\sqrt{3}$.其中正确的结论是①②③.