题目内容
9. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3$\sqrt{3}$.其中正确的结论是①②③.
如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3$\sqrt{3}$.其中正确的结论是①②③.
分析 连接OO′,如图,先利用旋转的性质得BO′=BO=4,∠OBO′=60°,再利用△ABC为等边三角形得到BA=BC,∠ABC=60°,则根据旋转的定义可判断△BO′A可以由△BOC绕点B逆时针旋转60°得到;接着证明△BOO′为等边三角形得到∠BOO′=60°,OO′=OB=4;根据旋转的性质得到AO′=OC=5,利用勾股定理的逆定理证明△AOO′为直角三角形,∠AOO′=90°,于是得到∠AOB=150°;最后利用S四边形AOBO′=S△AOO′+S△BOO′可计算出S四边形AOBO′=6+4$\sqrt{3}$.
解答  解:连接OO′,如图
解:连接OO′,如图
∵线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,
∴BO′=BO=4,∠OBO′=60°,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,则①正确;
∵BO′=BO=4,∠OBO′=60°,
∴△BOO′为等边三角形,
∴∠BOO′=60°,OO′=OB=4,所以②正确;
∵△BO′A可以由△BOC绕点B逆时针旋转60°得到,
∴AO′=OC=5,
在△AOO′中,∵OA=3,OO′=4,AO′=5,
∴OA2+OO′2=AO′2,
∴△AOO′为直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,所以③正确;
S四边形AOBO′=S△AOO′+S△BOO′=$\frac{1}{2}$×3×4+$\frac{\sqrt{3}}{4}$×42=6+4$\sqrt{3}$,所以④错误.
故答案为①②③.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质和勾股定理的逆定理.

| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
 如图,在扇形AOB中,∠AOB=45°,点C为OB的中点,以点C为圆心,以OC的长为半径画半圆交OA于点D,若OB=2,则阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.
如图,在扇形AOB中,∠AOB=45°,点C为OB的中点,以点C为圆心,以OC的长为半径画半圆交OA于点D,若OB=2,则阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.
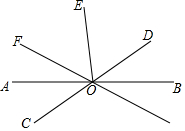 如图,已知直线AB、CD相交于点O,OE⊥AB,OA是∠COF的平分线,那么∠DOE=∠FOE,请说明理由.
如图,已知直线AB、CD相交于点O,OE⊥AB,OA是∠COF的平分线,那么∠DOE=∠FOE,请说明理由.