题目内容
2. 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求二次函数的解析式.
(2)请直接写出D点的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
分析 (1)由于已知抛物线与x轴两交点,则设交点式y=a(x+3)(x-1),然后把C(0,3)代入求出a的值即可得到抛物线解析式;
(2)通过解方程-x2-2x+3=3可得到D(-2,3);
(3)观察函数图象,写出一次函数图象在抛物线上方所对应的自变量的范围即可.
解答 解;(1)设二次函数的解析式为y=a(x+3)(x-1),
把C(0,3)代入得a×3×(-1)=3,解得a=-1.
所以抛物线解析式为y=-(x+3)(x-1),即y=-x2-2x+3;
(2)当y=3时,-x2-2x+3=3,解得x1=0,x2=-2.
则D(-2,3).
(3)观察函数图象得使一次函数值大于二次函数值的x的取值范围是x<-2或x>1.
点评 本题考查了抛物线与x轴的交点:由二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了二次函数与不等式.

练习册系列答案
相关题目
7.如图(1)是长方形纸片,∠DAC=20°将纸片沿AC折叠成图(2),再沿EC折叠成图(3),则图(3)中∠ACD为( )


| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
12.下列运算中,结果正确的是( )
| A. | (x2)3=x5 | B. | 3x2+2x2=5x4 | C. | x3•x3=x6 | D. | (x+y)2=x2+y2 |
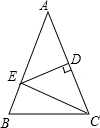 如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.