题目内容
7.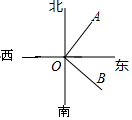 如图,在点O北偏东65°的某处有一点A,在点O南东20°的某处有一点B,则∠AOB的度数是95°.
如图,在点O北偏东65°的某处有一点A,在点O南东20°的某处有一点B,则∠AOB的度数是95°.
分析 根据方向角的定义,可得∠1,∠2,根据角的和差,课的答案.
解答 解:由题意,得
∠1=65°,∠2=20°.
由角的和差,得
∠AOB=∠3=180°-∠1-∠2=180°-65°-20°=95°,
故答案为:95°.
点评 本题考查了方向角,利用方向角的定义得出∠1,∠2是解题关键,又利用了角的和差.

练习册系列答案
相关题目
17.某班学生军训射击,有m人各打中a环,n人各打中b环,那么该班打中a环和b环学生的平均环数是( )
| A. | $\frac{a+b}{m+n}$ | B. | $\frac{1}{2}$($\frac{a}{m}$+$\frac{b}{n}$) | C. | $\frac{am+bn}{m+n}$ | D. | $\frac{1}{2}$(am+bn) |
18.计算-0.32÷0.5×2÷(-2)3的结果是( )
| A. | $\frac{9}{100}$ | B. | -$\frac{9}{100}$ | C. | $\frac{9}{200}$ | D. | -$\frac{9}{200}$ |
2.下列解方程过程中,变形正确的是( )
| A. | 由2x-1=3得2x=3-1 | |
| B. | 由$\frac{x}{3}$-$\frac{x}{2}$=1得2x-3x=6 | |
| C. | 由-5x=6得x=-$\frac{5}{6}$ | |
| D. | 由$\frac{x}{4}$+1=$\frac{3x+1}{0.1}$+1.2得$\frac{x}{4}$+1=$\frac{3x+1}{1}$+12 |
19.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
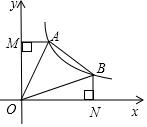 如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论:
如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论: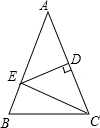 如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.