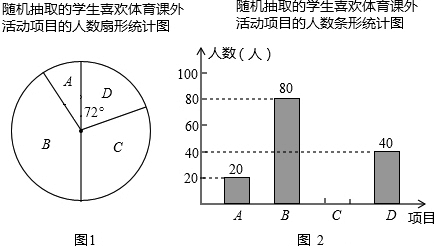
题目内容
9.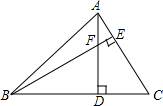 如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?
如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?
分析 先证出∠DBF=∠DAC,再证明△ABD是等腰直角三角形,得出BD=AD,由ASA证明△BDF≌△ADC,即可得出BF=AC=8cm.
解答 解:∵F是高AD和BE的交点,
∴∠FDB=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴BD=AD,
在△BDF和△ADC中,
$\left\{\begin{array}{l}{∠FDB=∠ADC}&{\;}\\{BD=AD}&{\;}\\{∠DBF=∠DAC}&{\;}\end{array}\right.$,
∴△BDF≌△ADC(ASA),
∴BF=AC=8cm.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握全等三角形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.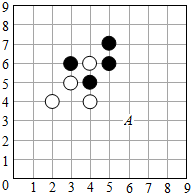 甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )
甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )
 甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )
甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )| A. | 黑(3,7);白(3,5) | B. | 黑(4,7);白(6,2) | C. | 黑(3,7);白(5,3) | D. | 黑(4,7);白(2,6) |
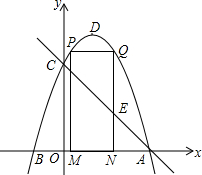 如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.
如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.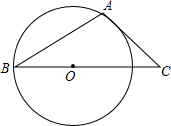 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的大小等于40.
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的大小等于40.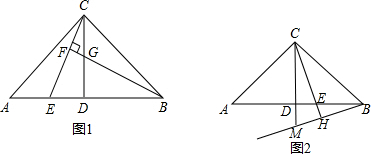
 如图,AB是⊙O的直径,P在BA的延长线上,过P作⊙O的切线,当D为$\widehat{AE}$中点时,试判断△PBC的形状.
如图,AB是⊙O的直径,P在BA的延长线上,过P作⊙O的切线,当D为$\widehat{AE}$中点时,试判断△PBC的形状.