题目内容
19.为推进阳光体育活动的开展,某学校决定开设以下体育课外活动项目:A.排球;B.乒乓球;C.篮球; D.羽毛球.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: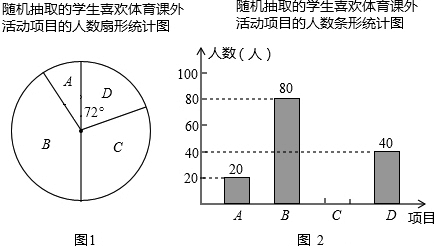
(1)这次被调查的学生共有200人;喜欢排球人数所占扇形圆心角是36°;
(2)请你将条形统计图补充完整;
(3)若甲、乙、丙、丁四位同学都喜欢乒乓球运动,现从这四名同学中任选两名进行对抗练习,求恰好选中乙、丙两位同学的概率(用树状图或列表法解答).
分析 (1)由题意可知这次被调查的学生共有40÷$\frac{72}{360}$=200;由题意可得喜欢排球人数所占扇形圆心角的大小为:$\frac{20}{200}$×360°=36°;
(2)首先求得C项目对应人数为:200-20-80-40=60(人),继而可补全条形统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中乙、丙两位同学的情况,再利用概率公式即可求得答案.
解答 解:(1)根据题意得:这次被调查的学生共有40÷$\frac{72}{360}$=200(人);喜欢排球人数所占扇形圆心角的大小为:$\frac{20}{200}$×360°=36°;
故答案为:200,36°;
(2)C项目对应人数为:200-20-80-40=60(人);
补充如图.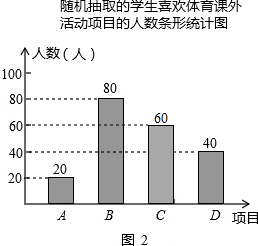
(3)列表如下:
| 甲 | 乙 | 丙 | 丁 | |
| 甲 | ﹨ | (乙,甲) | (丙,甲) | (丁,甲) |
| 乙 | (甲,乙) | ﹨ | (丙,乙) | (丁,乙) |
| 丙 | (甲,丙) | (乙,丙) | ﹨ | (丁,丙) |
| 丁 | (甲,丁) | (乙,丁) | (丙,丁) | ﹨ |
∴P(选中乙、丙)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
10.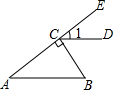 如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
 如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )| A. | 50° | B. | 40° | C. | 35° | D. | 25° |
14.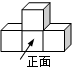 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )
 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )| A. | 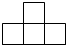 | B. |  | C. |  | D. | 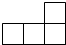 |
11.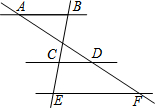 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )| A. | $\frac{36}{5}$ | B. | $\frac{24}{5}$ | C. | $\frac{15}{2}$ | D. | $\frac{9}{2}$ |
9.关于x的方程x2-3x-a=0有实数根,则a的取值可能是( )
| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
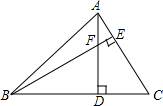 如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?
如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?