题目内容
1. 如图,AB是⊙O的直径,P在BA的延长线上,过P作⊙O的切线,当D为$\widehat{AE}$中点时,试判断△PBC的形状.
如图,AB是⊙O的直径,P在BA的延长线上,过P作⊙O的切线,当D为$\widehat{AE}$中点时,试判断△PBC的形状.
分析 首先连接OD,由过点P作⊙O的切线,切点为D,可得OD⊥PC,又由点D为弧AE的中点,根据垂径定理即可求得OD⊥AE,AB是⊙O的直径,易证得OD∥BC,即可证得∠C=90°,判定△PBC是直角三角形.
解答 解:△PBC是直角三角形.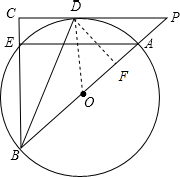 理由:连接OD,
理由:连接OD,
∵PD是⊙O的切线,
∴OD⊥PD,
∵点D为弧AE的中点,
∴OD⊥AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴AE⊥BE,
∴OD∥BE,
∴BC⊥PC,
即△PBC是直角三角形.
点评 此题考查了切线的性质、垂径定理、圆周角定理以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
6.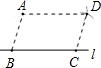 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
13.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. | 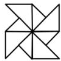 | C. |  | D. |  |
10.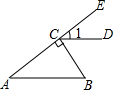 如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
 如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=50°,则∠1等于( )| A. | 50° | B. | 40° | C. | 35° | D. | 25° |
11.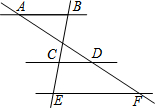 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )| A. | $\frac{36}{5}$ | B. | $\frac{24}{5}$ | C. | $\frac{15}{2}$ | D. | $\frac{9}{2}$ |
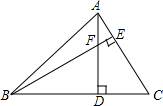 如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?
如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?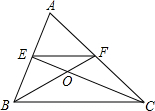 如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )
如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )