题目内容
4.已知二次函数y=x2+mx+n.(1)设m=-2,当-3≤x≤0时,求二次函数的最小值(用字母表示);
(2)若-3≤x≤0时二次函数的最小值为-4,求m、n应满足的关系?
分析 (1)当m=-2时,y=x2+mx+n=x2-2x+n,根据对称轴是x=1,可得当-3≤x≤0时,y单调递减,据此求出二次函数的最小值即可.
(2)二次函数y=x2+mx+n的对称轴是x=-$\frac{m}{2}$,分三种情况讨论:①当-$\frac{m}{2}$≤-3时;②当-3<-$\frac{m}{2}$<0时;③当-$\frac{m}{2}$≥0时;根据二次函数的最小值为-4,判断出m、n应满足的关系即可.
解答 解:(1)当m=-2时,
y=x2+mx+n=x2-2x+n,
对称轴是:x=-$\frac{-2}{2×1}=1$,
∵二次函数开口向上,
∴当-3≤x≤0时,y单调递减,
∴当x=0时,
ymin=02-2×0+n=n,
即当-3≤x≤0时,二次函数的最小值是n.
(2)二次函数y=x2+mx+n的对称轴是x=-$\frac{m}{2}$,
①当-$\frac{m}{2}$≤-3时,即m≥6时,
-3≤x≤0时,y单调递增,
∴当x=-3时,
ymin=(-3)2+m×(-3)+n=-3m+n+9=-4,
∴n=3m-13.
②当-3<-$\frac{m}{2}$<0时,即0<m<6时,
当x=-$\frac{m}{2}$时,
ymin=$\frac{4n{-m}^{2}}{4}$=-4,
∴n=$\frac{{m}^{2}}{4}-4$.
③当-$\frac{m}{2}$≥0时,即m≤0时,
-3≤x≤0时,y单调递减,
∴当x=0时,
ymin=02+m×0+n=n=-4,
∴n=-4.
点评 此题主要考查了二次函数的最值的求法,要熟练掌握,解答此题的关键是要明确:确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.

| A. | 0 | B. | 2.5 | C. | 3 | D. | 5 |
| A. |  | B. |  | C. |  | D. |  |
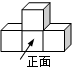 如图,由4个正方体组成的几何体的左视图是( )
如图,由4个正方体组成的几何体的左视图是( )| A. | 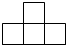 | B. |  | C. |  | D. | 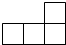 |
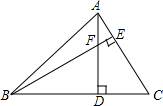 如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?
如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?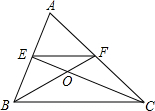 如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )
如图,在△ABC中,点E,F分别为AB,AC的中点,连接CE,BF,相交于点O.若△OEF的面积为1,则△ABC的面积为( )