题目内容
17．
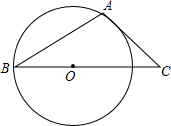如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心，若∠B=25°，则∠C的大小等于40．
分析 连接OA，根据切线的性质，即可求得∠C的度数．
解答 
解：如图，连接OA，
∵AC是⊙O的切线，
∴∠OAC=90°，
∵OA=OB，
∴∠B=∠OAB=25°，
∴∠AOC=50°，
∴∠C=40°．
故答案为：40．
点评 本题考查了圆的切线性质，以及等腰三角形的性质，已知切线时常用的辅助线是连接圆心与切点．
练习册系列答案
相关题目
11．a的相反数是（ ）
| A． | |a| | B． | $\frac{1}{a}$ | C． | -a | D． | $\sqrt{a}$ |
8．
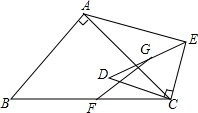如图，△ABC和△CDE均为等腰直角三角形，∠BAC=∠DCE=90°，且AC=2CE，F、G分别为BC、DE边上的中点，连接AE、FG，AE=3，则FG的长度为（ ）
如图，△ABC和△CDE均为等腰直角三角形，∠BAC=∠DCE=90°，且AC=2CE，F、G分别为BC、DE边上的中点，连接AE、FG，AE=3，则FG的长度为（ ）| A． | $\frac{3}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\frac{3\sqrt{2}}{2}$ |
5．已知x，y是二元一次方程式组$\left\{\begin{array}{l}{2x+y=10}\\{2y-x=6}\end{array}\right.$的解，则3x-y的算术平方根为（ ）
| A． | ±2 | B． | 4 | C． | $\sqrt{2}$ | D． | 2 |
2．下面四个图形是多面体的展开图，其中不是棱柱的展开图的是（ ）
| A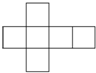． |  | B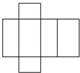． |  | C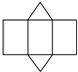． |  | D． |  |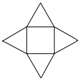
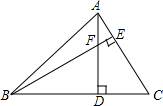如图所示，在△ABC中，∠ABC=45°，AC=8cm，F是高AD和BE的交点，则BF的长是多少？
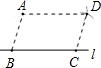如图，点A是直线l外一点，在l上取两点B，C，分别以A，C为圆心，BC，AB长为半径画弧，两弧交于点D，分别连接AB、AD、CD，则四边形ABCD一定是（ ）