题目内容
14.已知:在△ABC中,AC=BC,∠ACD=∠BCD=45°,点E是AB边上一点.(1)求证:CD⊥AB;
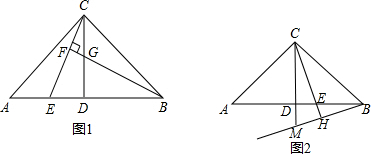
(2)若BF⊥CE于点F,交CD于点G(如图1),求证:AE=CG.
(3)若将CE移至(如图2)位置,此时,BH⊥CE,垂足为点H,交CD的延长线于点M,找出此时图中与AE相等的线段.
分析 (1)由等腰三角形的三线合一性质即可得出结论;
(2)先证出∠ACE=∠CBG,再由ASA证明△ACE≌△CBG,得出对应边相等即可;
(3)先证出∠CEA=∠CMB,再由AAS证明△ACE≌△BCM,得出对应边相等即可.
解答 (1)证明:∵AC=BC,∠ACD=∠BCD=45°,
∴CD⊥AB(三线合一);
(2)证明:∵AC=BC,∠ACD=∠BCD=45°,
∴∠ACB=90°,
∴∠A=∠ABC=45°,∠ACE=90°-∠BCF,
∵BF⊥CE,
∴∠CFB=90°,
∴∠CBG=90°-∠BCF,
∴∠ACE=∠CBG,
在△ACE和△CBG中,
$\left\{\begin{array}{l}{∠A=∠BCG=45°}&{\;}\\{AC=BC}&{\;}\\{∠ACE=∠BCG}&{\;}\end{array}\right.$,
∴△ACE≌△CBG(ASA),
∴AE=CG;
(3)解:CM=AE;理由:
∵CD⊥AB,BH⊥CE,
∴∠CDE=∠CHM=90°,
∴∠DCE+∠CEA=90°,∠DCE+∠CMB=90°,
∴∠CEA=∠CMB,
在△ACE和△BCM中,
$\left\{\begin{array}{l}{∠A=∠BCM=45°}&{\;}\\{∠CEA=∠CMB}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△ACE≌△BCM(AAS),
∴CM=AE.
点评 本题考查了全等三角形的判定与性质、等腰三角形的性质;熟练掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
8.把代数式3x3-12x2+12x分解因式,结果正确的是( )
| A. | 3x(x2-4x+4) | B. | 3x(x-4)2 | C. | 3x(x+2)(x-2) | D. | 3x(x-2)2 |
5.已知x,y是二元一次方程式组$\left\{\begin{array}{l}{2x+y=10}\\{2y-x=6}\end{array}\right.$的解,则3x-y的算术平方根为( )
| A. | ±2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2 |
2.下面四个图形是多面体的展开图,其中不是棱柱的展开图的是( )
| A. | 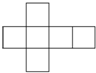 | B. | 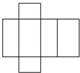 | C. | 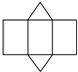 | D. |  |
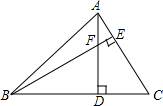 如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少?
如图所示,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是多少? 已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.
已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.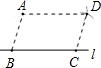 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )